ГДЗ по Математике 6 Класс Часть 1 Номер 2.221 Виленкин, Жохов — Подробные Ответы

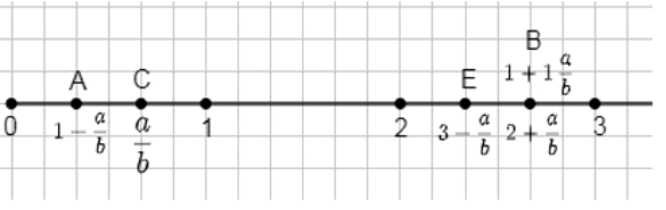
Отметьте на координатной прямой (рис. 2.6) точки, координаты которых равны:
а) \(1-\frac{a}{b}\);
б) \(2+\frac{a}{b}\);
в) \(3-\frac{a}{b}\).

Точка с координатой \(1 — \frac{a}{b}\) находится слева от 1, ближе к 0, это точка \(A\).

Точка с координатой \(2 + \frac{a}{b}\) находится справа от 2, ближе к 3, это точка \(B\).

Точка с координатой \(3 — \frac{a}{b}\) находится слева от 3, ближе к 2, это точка \(E\).

1) Координата точки \(A\) равна \(1 — \frac{a}{b}\). Это означает, что мы начинаем от точки 1 на числовой оси и сдвигаемся влево на величину \(\frac{a}{b}\). Поскольку \(\frac{a}{b}\) — положительное число, вычитание уменьшает значение, поэтому точка \(A\) расположена между 0 и 1, ближе к 1, но левее него. На чертеже видно, что точка \(A\) находится именно в этой позиции, что соответствует её координате.

2) Для точки \(B\) координата задана как \(1 + 1 \cdot \frac{a}{b} = 1 + \frac{a}{b}\). Это значит, что мы начинаем от точки 1 и сдвигаемся вправо на величину \(\frac{a}{b}\). Таким образом, точка \(B\) расположена между 1 и 2, ближе к 1, но правее него. В формуле, приведённой на рисунке, показано, что \(B\) равна \(2 + \frac{a}{b}\), что означает, что она сдвинута вправо от точки 2 на \(\frac{a}{b}\). На числовой оси это подтверждается расположением точки \(B\ справа от 2.

3) Точка \(E\) имеет координату \(3 — \frac{a}{b}\). Это означает, что мы начинаем от точки 3 и сдвигаемся влево на величину \(\frac{a}{b}\). Поскольку \(\frac{a}{b}\) положительна, вычитание уменьшает значение, поэтому точка \(E\) находится между 2 и 3, ближе к 3, но левее него. На рисунке видно, что \(E\) расположена именно в этой позиции, что совпадает с заданной координатой. Таким образом, все точки отмечены на числовой оси согласно их координатам, учитывая направление и величину сдвига от целых чисел.