ГДЗ по Математике 6 Класс Часть 1 Номер 2.163 Виленкин, Жохов — Подробные Ответы

На координатной прямой отмечены точки \(N\left(\frac{1}{n}\right)\), \(M\left(\frac{1}{m}\right)\) и \(K\left(\frac{1}{k}\right)\) (рис. 2.5). Отметьте на координатной прямой точку с координатами:

а) \(1+\frac{1}{n}\);

б) \(1-\frac{1}{m}\);

в) \(\frac{1}{k}-\frac{1}{n}\);

г) \(\frac{1}{n}+\frac{1}{k}\).

а) Чтобы отметить точку \(1 + \frac{1}{n}\), надо от точки \(M\left(\frac{1}{m}\right)\) отсчитать вправо отрезок \(\frac{1}{n}\).

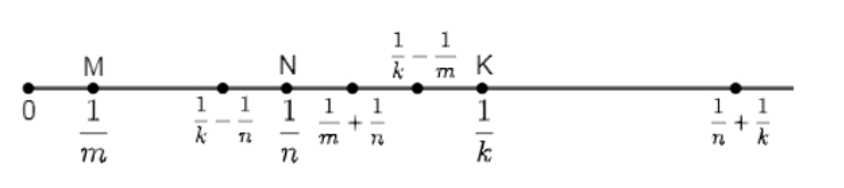
б) Чтобы отметить точку \(1 — \frac{1}{m}\), надо от точки \(K\left(\frac{1}{k}\right)\) отсчитать влево отрезок \(\frac{1}{m}\).

в) Чтобы отметить точку \(\frac{1}{k} — \frac{1}{n}\), надо от точки \(K\left(\frac{1}{k}\right)\) отсчитать влево отрезок \(\frac{1}{n}\).

г) Чтобы отметить точку \(\frac{1}{n} + \frac{1}{k}\), надо от точки \(N\left(\frac{1}{n}\right)\) отсчитать вправо отрезок \(\frac{1}{k}\).

1) Чтобы отметить точку \(1 + \frac{1}{n}\) на координатной прямой, сначала нужно понять, где находится точка \(M\) с координатой \(\frac{1}{m}\). Эта точка уже отмечена на прямой. Далее, чтобы получить координату \(1 + \frac{1}{n}\), нужно от точки \(M\) двигаться вправо, так как прибавление к числу означает движение вправо по оси. Расстояние, на которое нужно сдвинуться, равно \(\frac{1}{n}\). Таким образом, от точки \(M\) отсчитываем вправо отрезок длиной \(\frac{1}{n}\), и получаем искомую точку.

2) Для отметки точки \(1 — \frac{1}{m}\) важно сначала найти точку \(K\) с координатой \(\frac{1}{k}\). Так как выражение содержит вычитание, то нужно от точки \(K\) двигаться влево, ведь вычитание уменьшает значение. Расстояние, которое надо отсчитать влево, равно \(\frac{1}{m}\). Следовательно, начиная от точки \(K\), отсчитываем влево отрезок длиной \(\frac{1}{m}\), и таким образом отмечаем точку \(1 — \frac{1}{m}\).

3) Чтобы отметить точку \(\frac{1}{k} — \frac{1}{n}\), нужно сначала найти точку \(K\) с координатой \(\frac{1}{k}\). Поскольку здесь также есть вычитание, необходимо двигаться влево от точки \(K\) на расстояние \(\frac{1}{n}\). Отсчитав влево отрезок длиной \(\frac{1}{n}\), получим точку с координатой \(\frac{1}{k} — \frac{1}{n}\).

4) Для отметки точки \(\frac{1}{n} + \frac{1}{k}\) сначала находим точку \(N\) с координатой \(\frac{1}{n}\). При сложении необходимо двигаться вправо от точки \(N\) на расстояние, равное \(\frac{1}{k}\). Отсчитав вправо отрезок длиной \(\frac{1}{k}\), получаем точку с координатой \(\frac{1}{n} + \frac{1}{k}\).