
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 2.140 Виленкин, Жохов — Подробные Ответы
Используя транспортир, разделите окружность: а) на 6 равных частей; б) на 3 равные части. Соедините последовательно получившиеся точки отрезками. Измерьте стороны и углы построенного многоугольника. Сделайте предположение.
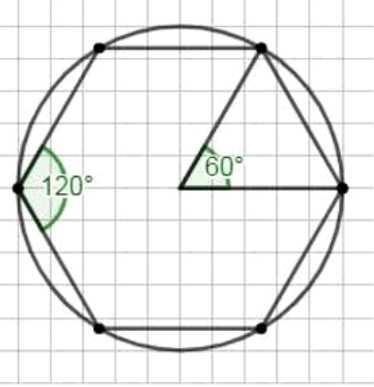
а) Окружность разделена на 6 равных частей, каждый центральный угол равен \( \frac{360^\circ}{6} = 60^\circ \). При соединении точек получается правильный шестиугольник с сторонами по 2,5 см и внутренними углами по 120°.
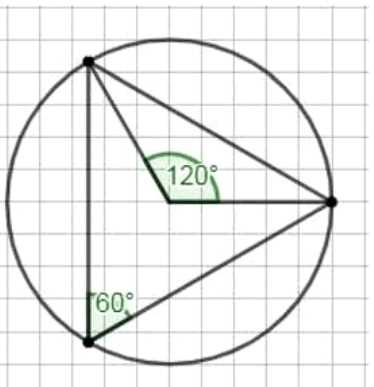
б) Окружность разделена на 3 равные части, каждый центральный угол равен \( \frac{360^\circ}{3} = 120^\circ \). При соединении точек получается правильный треугольник с сторонами по 4,3 см и внутренними углами по 60°.
Вывод: если окружность разделить на равные части и соединить эти точки отрезками, получается правильный многоугольник с равными сторонами и равными углами.
1) При делении окружности на 6 равных частей каждый центральный угол равен \( \frac{360^\circ}{6} = 60^\circ \). Это значит, что радиусы, проведённые к точкам деления, образуют между собой угол 60 градусов. Если соединить последовательно эти точки отрезками, то получим правильный шестиугольник. В правильном шестиугольнике все стороны равны, что подтверждается измерением сторон, равных 2,5 см. Внутренний угол правильного шестиугольника равен 120 градусам, что также совпадает с измерениями углов многоугольника на рисунке. Таким образом, построенный многоугольник является правильным шестиугольником.
2) При делении окружности на 3 равные части каждый центральный угол равен \( \frac{360^\circ}{3} = 120^\circ \). Радиусы, проведённые к точкам деления, образуют угол 120 градусов. Соединяя эти точки отрезками, получаем правильный треугольник. В правильном треугольнике все стороны равны, что подтверждается измерением сторон по 4,3 см. Внутренний угол правильного треугольника равен 60 градусам, что совпадает с измерениями углов многоугольника на рисунке. Следовательно, построенный многоугольник — правильный треугольник.
Вывод: если окружность разделить на равные части, то центральные углы между радиусами будут равны. Соединение точек деления отрезками создаёт правильный многоугольник, у которого равны все стороны и равны все углы. Это объясняется тем, что равные центральные углы обеспечивают равенство дуг окружности, а следовательно, и равенство сторон многоугольника. Внутренние углы правильного многоугольника можно вычислить по формуле \( \frac{(n-2) \cdot 180^\circ}{n} \), где \( n \) — число сторон. Таким образом, построение правильных многоугольников сводится к равномерному делению окружности и соединению точек деления.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!