ГДЗ по Математике 6 Класс Часть 1 Номер 1.71 Виленкин, Жохов — Подробные Ответы

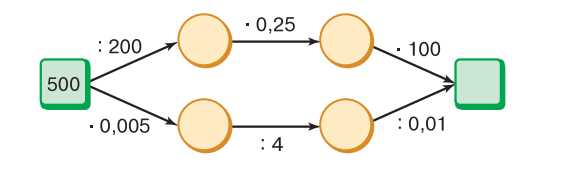
Выполните вычисления. Объясните, почему получается одинаковый ответ.

Вычислим по двум путям:

Первый путь:
\(500 : 200 = 2{,}5\),
\(2{,}5 \cdot 0{,}25 = 0{,}625\),
\(0{,}625 \cdot 100 = 62{,}5\).

Второй путь:
\(500 \cdot 0{,}005 = 2{,}5\),
\(2{,}5 : 4 = 0{,}625\),
\(0{,}625 : 0{,}01 = 62{,}5\).

Мы знаем, что:
\(\frac{1}{200} = 0{,}005\),
\(\frac{1}{4} = 0{,}25\),
\(\frac{1}{100} = 0{,}01\).

Умножение на \(0{,}005\) означает нахождение \(\frac{1}{200}\) числа,
умножение на \(0{,}25\) — нахождение \(\frac{1}{4}\) числа,
умножение на \(100\) — нахождение \(\frac{1}{100}\) числа.

Оба способа дают одинаковый результат, потому что операции деления и умножения связаны через обратные величины, и последовательность преобразований эквивалентна.

1. Рассмотрим первый способ вычисления. Сначала делим число 500 на 200. Деление на 200 можно представить как деление на 2, а затем на 100, или наоборот. В данном случае \(500 : 200 = 2{,}5\). Это число затем умножаем на 0,25, что эквивалентно нахождению четверти от числа, так как \(0{,}25 = \frac{1}{4}\). Таким образом, \(2{,}5 \cdot 0{,}25 = 0{,}625\). Далее, умножаем результат на 100, что увеличивает число в сто раз: \(0{,}625 \cdot 100 = 62{,}5\).

2. Второй способ начинается с умножения 500 на 0,005. Число 0,005 — это десятичное представление дроби \(\frac{1}{200}\), то есть умножение на 0,005 эквивалентно нахождению одной двухсотой части числа. Получаем \(500 \cdot 0{,}005 = 2{,}5\). Далее число 2,5 делим на 4: \(2{,}5 : 4 = 0{,}625\). Деление на 4 — это нахождение четверти числа. Последний шаг — деление на 0,01, которое равно делению на сотую часть, то есть умножению на 100: \(0{,}625 : 0{,}01 = 62{,}5\).

3. Оба способа дают одинаковый результат, потому что операции деления и умножения взаимно обратны и связаны через дробные величины. Умножение на \(0{,}005\) эквивалентно делению на 200, а умножение на \(0{,}25\) — нахождению четверти числа. При этом, умножение на 100 и деление на 0,01 — операции, обратные друг другу. Именно поэтому последовательность действий в первом и втором способах, хотя и разная, приводит к одному и тому же числу \(62{,}5\). Это демонстрирует взаимосвязь между дробями и десятичными дробями, а также свойства умножения и деления.