
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 1.52 Виленкин, Жохов — Подробные Ответы
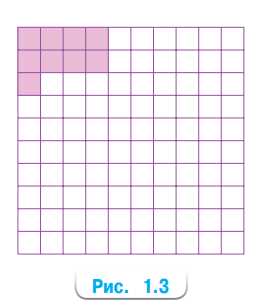
Квадрат на рисунке 1.3 разбит на 100 долей. Найдите площадь всего квадрата, если закрашено 20,25 см².
Закрашено 9 долей, площадь которых равна \(20,25 \text{ см}^2\).
Площадь одной доли: \(20,25 : 9 = 2,25 \text{ см}^2\).
Всего долей 100, значит площадь всего квадрата: \(2,25 \cdot 100 = 225 \text{ см}^2\).
Ответ: \(225 \text{ см}^2\).
Закрашено 9 долей, площадь которых равна \(20,25 \text{ см}^2\). Чтобы найти площадь одной доли, нужно общую площадь закрашенных частей разделить на количество этих долей. Выполним деление: \(20,25 : 9 = 2,25 \text{ см}^2\). Это означает, что каждая доля занимает площадь \(2,25 \text{ см}^2\).
Квадрат разбит на 100 равных долей, значит общая площадь квадрата равна площади одной доли, умноженной на 100. Используем найденное значение площади одной доли и умножаем: \(2,25 \cdot 100 = 225 \text{ см}^2\). Таким образом, площадь всего квадрата составляет \(225 \text{ см}^2\).
Итог: зная площадь нескольких долей и их количество, мы нашли площадь одной доли, а затем умножили её на общее количество долей, чтобы получить площадь всего квадрата. Это стандартный способ решения задач, связанных с делением фигур на равные части и вычислением общей площади. Ответ: \(225 \text{ см}^2\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!