ГДЗ по Математике 6 Класс Часть 1 Номер 1.156 Виленкин, Жохов — Подробные Ответы

 Используя линейку и транспортир, постройте треугольник \(MNK\), у которого:  

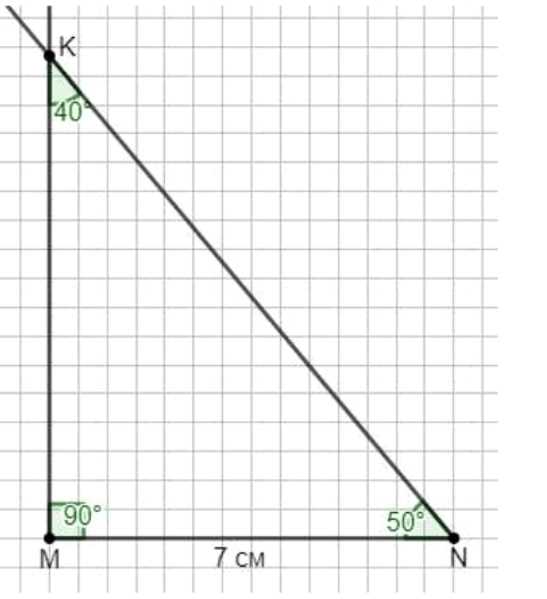
а) угол \(M\) равен \(90^\circ\), сторона \(MN\) равна \(7\) см и угол \(K\) равен \(40^\circ\);  

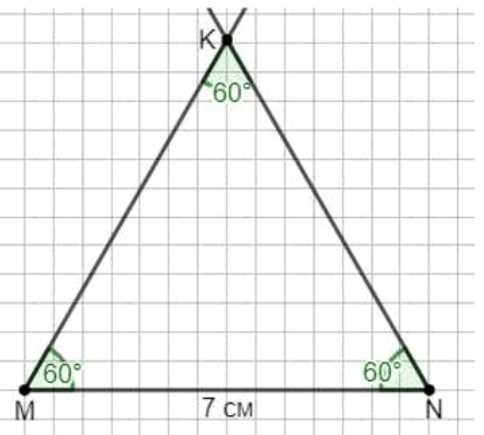
б) угол \(M\) равен \(60^\circ\), сторона \(MN\) равна \(7\) см и угол \(K\) равен \(60^\circ\);  

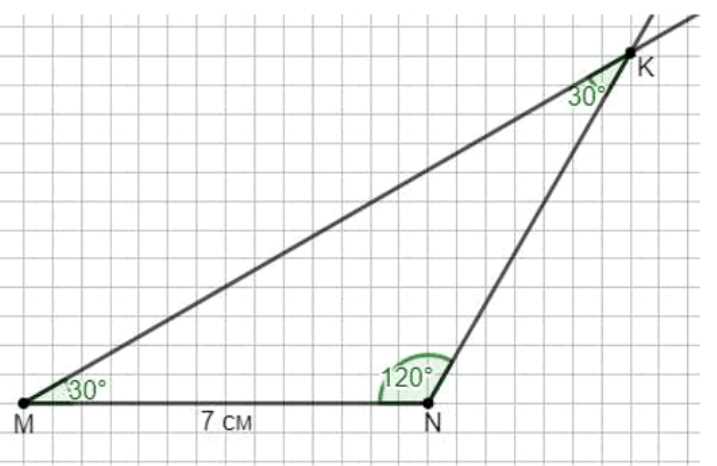
в) угол \(M\) равен \(30^\circ\), сторона \(MN\) равна \(7\) см и угол \(K\) равен \(30^\circ\). Определите вид треугольников.

а) Найдём угол \(N\): \(180-(90+40)=50^\circ\). Строим отрезок \(MN=7\) см, от луча \(MN\) откладываем угол \(M=90^\circ\), от луча \(NM\) — угол \(N=50^\circ\); продолжая стороны до пересечения, получаем точку \(K\). Вид: прямоугольный разносторонний треугольник.

б) Найдём угол \(N\): \(180-(60+60)=60^\circ\). Строим \(MN=7\) см, откладываем от \(MN\) угол \(M=60^\circ\) и от \(NM\) угол \(N=60^\circ\); пересечение даёт \(K\). Вид: остроугольный равносторонний треугольник.

в) Найдём угол \(N\): \(180-(30+30)=120^\circ\). Строим \(MN=7\) см, откладываем от \(MN\) угол \(M=30^\circ\) и от \(NM\) угол \(N=120^\circ\); пересечение даёт \(K\). Вид: тупоугольный равнобедренный треугольник.

а) Сначала используем основное свойство треугольника: сумма внутренних углов равна \(180^\circ\). При известных углах \(M=90^\circ\) и \(K=40^\circ\) находим третий угол: \(N=180^\circ-(90^\circ+40^\circ)=50^\circ\). Для построения берём линейку и откладываем на бумаге отрезок \(MN=7\) см. Далее прикладываем транспортир к точке \(M\) на луч \(MN\) и отмечаем луч, образующий с \(MN\) угол \(90^\circ\) — это перпендикуляр к \(MN\). Затем к точке \(N\) прикладываем транспортир на луч \(NM\) и отмечаем луч, образующий с \(NM\) угол \(50^\circ\). Продлеваем обе отмеченные полупрямые до их пересечения и получаем точку \(K\). Проверка: углы при \(M\) и \(K\) действительно \(90^\circ\) и \(40^\circ\), а при \(N\) — \(50^\circ\); сумма равна \(180^\circ\). По виду: один угол прямой, остальные острые и все три угла различны, следовательно, треугольник прямоугольный разносторонний.

б) Применим то же свойство суммы углов: при \(M=60^\circ\) и \(K=60^\circ\) имеем \(N=180^\circ-(60^\circ+60^\circ)=60^\circ\). Построение: откладываем отрезок \(MN=7\) см. В точке \(M\) по транспорти­ру строим луч, который с \(MN\) образует угол \(60^\circ\). В точке \(N\) по транспорти­ру строим луч, который с \(NM\) образует угол \(60^\circ\). Продлеваем эти лучи до пересечения и получаем вершину \(K\). Проверка: каждый из углов треугольника равен \(60^\circ\), их сумма \(180^\circ\), а значит, построение корректно. По виду: все углы острые и равны, следовательно, треугольник остроугольный равносторонний; как следствие, все его стороны равны, но базовый отрезок \(MN\) фиксирован \(7\) см, значит каждая сторона равна \(7\) см.

в) Снова пользуемся суммой углов: при \(M=30^\circ\) и \(K=30^\circ\) находим \(N=180^\circ-(30^\circ+30^\circ)=120^\circ\). Строим основу \(MN=7\) см. В точке \(M\) на луче \(MN\) откладываем угол \(30^\circ\). В точке \(N\) на луче \(NM\) откладываем угол \(120^\circ\) (это угол, превышающий прямой; визуально — внутренний угол при вершине \(N\), распахнутый на \(120^\circ\) от стороны \(NM\)). Продлеваем полученные лучи до их пересечения и отмечаем точку \(K\). Проверка: углы при вершинах \(M\), \(N\), \(K\) равны \(30^\circ\), \(120^\circ\), \(30^\circ\) соответственно, сумма равна \(180^\circ\). По виду: один угол тупой (\(120^\circ\)), два остальных острые и равные (\(30^\circ\) и \(30^\circ\)), следовательно, треугольник тупоугольный равнобедренный, причём боковые стороны \(MK\) и \(KN\) равны, так как при основании \(MN\) прилегающие углы равны.