
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 1.155 Виленкин, Жохов — Подробные Ответы
Используя линейку и транспортир, постройте треугольник \(MNK\), у которого:
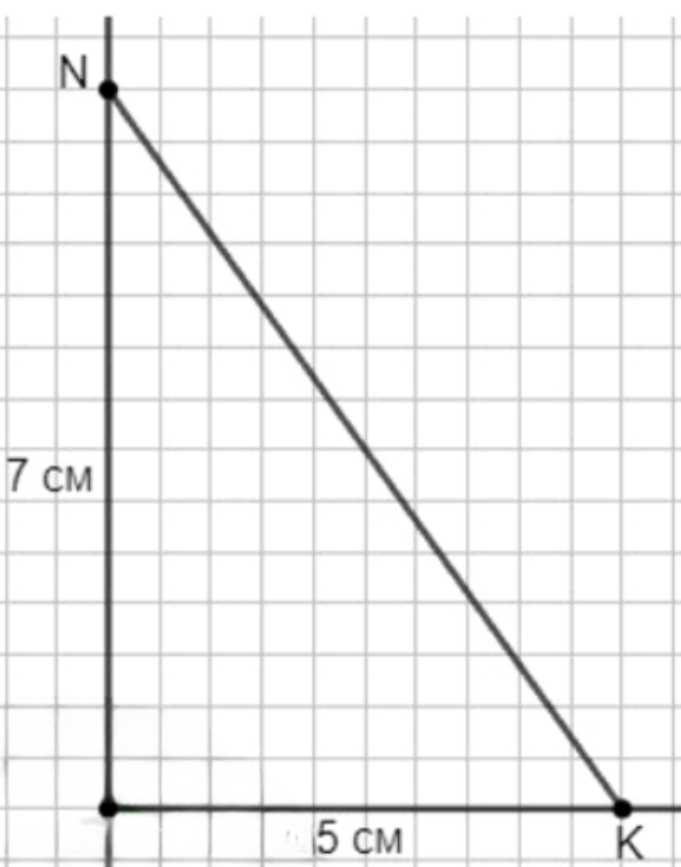
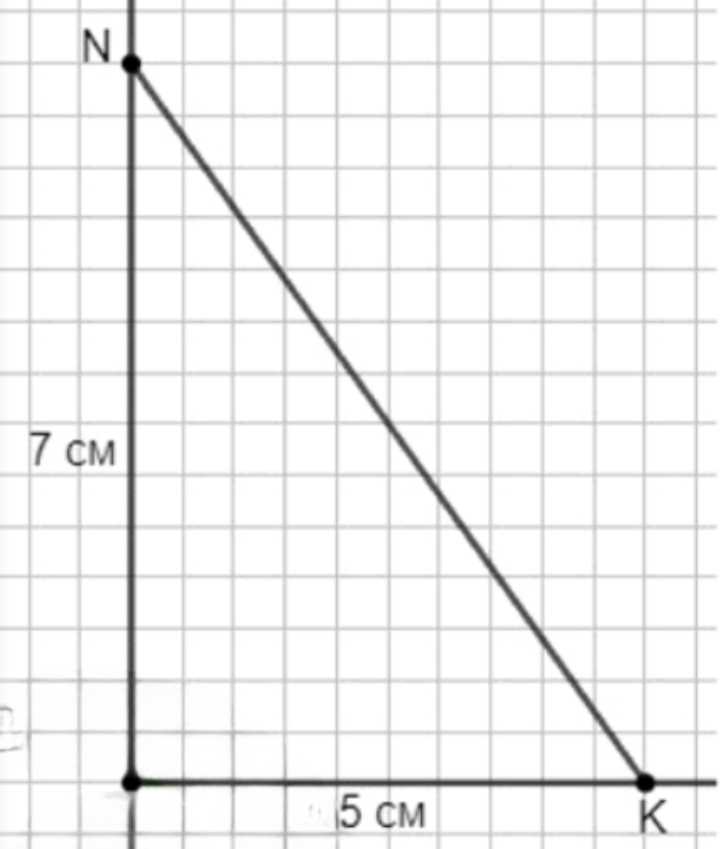
а) угол \(M\) равен \(90^\circ\), сторона \(MN\) равна \(7\) см и \(MK\) равна \(5\) см;
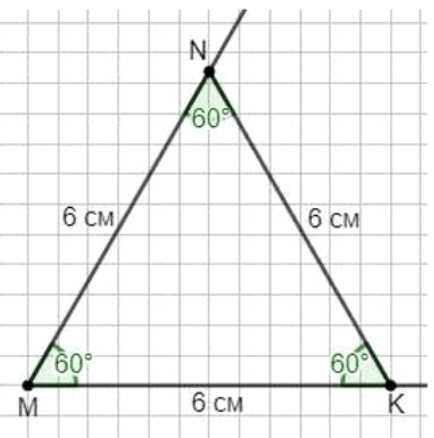
б) угол \(M\) равен \(60^\circ\), а стороны \(MN\) и \(MK\) равны по \(6\) см;
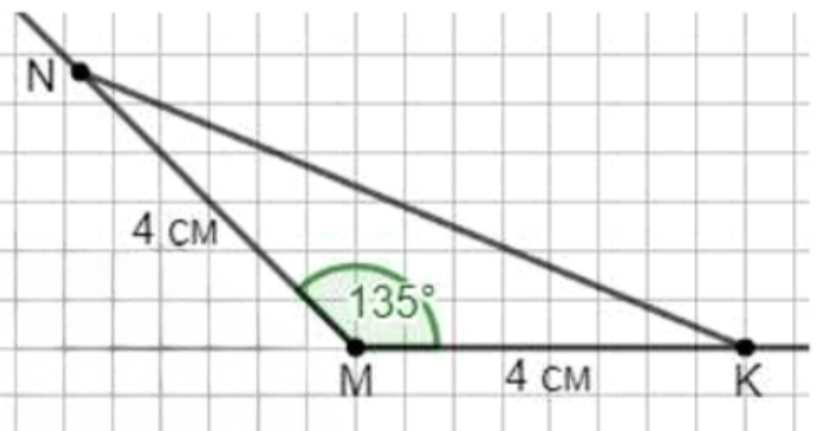
в) угол \(M\) равен \(135^\circ\), а стороны \(MN\) и \(MK\) равны по \(4\) см. Определите вид треугольников.
а) Построим угол \(M = 90^\circ\). Отложим от точки \(M\) отрезки \(MN = 7\) см и \(MK = 5\) см. Соединим точки \(N\) и \(K\). Получился прямоугольный разносторонний треугольник \(MNK\), так как угол \(M\) прямой, а стороны \(MN\) и \(MK\) разные.
б) Построим угол \(M = 60^\circ\). Отложим от точки \(M\) отрезки \(MN = 6\) см и \(MK = 6\) см. Соединим точки \(N\) и \(K\). Получился остроугольный равносторонний треугольник \(MNK\), так как все стороны равны и угол \(M = 60^\circ\).
в) Построим угол \(M = 135^\circ\). Отложим от точки \(M\) отрезки \(MN = 4\) см и \(MK = 4\) см. Соединим точки \(N\) и \(K\). Получился тупоугольный равнобедренный треугольник \(MNK\), так как угол \(M > 90^\circ\) и стороны \(MN\) и \(MK\) равны.
1) В первом случае нам дан угол \(M\), равный \(90^\circ\). Это означает, что угол прямой. С помощью транспортира мы точно откладываем угол \(90^\circ\) в точке \(M\). Затем на сторонах угла от точки \(M\) откладываем отрезки: \(MN = 7\) см и \(MK = 5\) см. Поскольку стороны разные, треугольник будет разносторонним. Соединяя точки \(N\) и \(K\), мы получаем треугольник \(MNK\), у которого угол при вершине \(M\) прямой. Таким образом, треугольник является прямоугольным и разносторонним.
2) Во втором случае угол \(M\) равен \(60^\circ\), что характерно для равностороннего треугольника, где все углы равны \(60^\circ\). С помощью транспортира строим угол \(60^\circ\) в точке \(M\). Затем на сторонах угла от точки \(M\) откладываем отрезки \(MN = 6\) см и \(MK = 6\) см, то есть равные по длине. Соединяя точки \(N\) и \(K\), получаем треугольник \(MNK\) с равными сторонами \(MN = MK = NK\) и углами по \(60^\circ\). Такой треугольник является остроугольным и равносторонним.
3) В третьем случае угол \(M\) равен \(135^\circ\), что больше \(90^\circ\), следовательно, угол тупой. С помощью транспортира строим угол \(135^\circ\) в точке \(M\). Затем на сторонах угла от точки \(M\) откладываем равные отрезки \(MN = 4\) см и \(MK = 4\) см. Соединяя точки \(N\) и \(K\), получаем треугольник \(MNK\), у которого угол при вершине \(M\) тупой, а стороны \(MN\) и \(MK\) равны. Следовательно, треугольник является тупоугольным и равнобедренным.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!