ГДЗ по Математике 6 Класс Часть 1 Номер 1.154 Виленкин, Жохов — Подробные Ответы

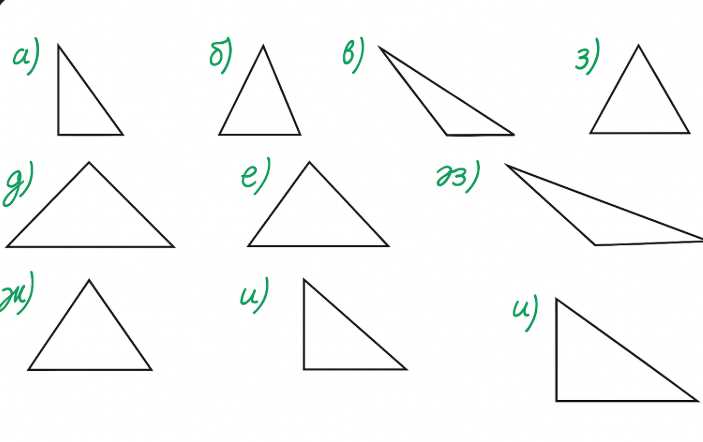
Нарисуйте треугольник:  

а) прямоугольный;  

б) остроугольный;  

в) тупоугольный;  

г) равносторонний;  

д) равнобедренный;  

е) разносторонний;  

ж) тупоугольный и равнобедренный;  

з) остроугольный и равнобедренный;  

и) прямоугольный и равнобедренный.

а) Прямоугольный: один угол равен \(90^\circ\).

б) Остроугольный: все три угла острые, каждый \(<90^\circ\).

в) Тупоугольный: один угол тупой, \(>90^\circ\).

г) Равносторонний: все стороны равны, значит все углы по \(60^\circ\).

д) Равнобедренный: две стороны равны, при основании равные углы.

е) Разносторонний: все три стороны различны, углы попарно различны.

ж) Тупоугольный и равнобедренный: две стороны равны и один угол \(>90^\circ\).

з) Остроугольный и равнобедренный: две стороны равны, все углы \(<90^\circ\).

и) Прямоугольный и равнобедренный: один угол \(90^\circ\), равные катеты, острые углы по \(45^\circ\).

а) Прямоугольный: в треугольнике один угол должен быть ровно \(90^\circ\). Для построения удобно провести отрезок-основание, из одной из его крайних точек восстановить перпендикуляр с помощью угольника или окружности (радиусом к другой точке основания) и отметить вершину на этом перпендикуляре. Тогда получаются катеты, смежные к прямому углу, и гипотенуза напротив него. Сумма углов треугольника равна \(180^\circ\), значит два оставшихся угла прямоугольного треугольника в сумме дают \(90^\circ\).

б) Остроугольный: требуется, чтобы каждый из трех углов был острым, то есть меньше \(90^\circ\). Достаточно взять произвольный треугольник, у которого высоты пересекаются внутри фигуры; практический способ — построить три стороны так, чтобы ни одна не «распахивала» угол более \(90^\circ\). Например, проведите основание, из его концов поднимите лучи под углами \(40^\circ\) и \(60^\circ\) и отметьте их пересечение. Проверка: если самый большой угол меньше \(90^\circ\), то треугольник остроугольный.

в) Тупоугольный: один угол должен быть больше \(90^\circ\). Постройте основание и из одной его точки отложите угол \(>90^\circ\), например \(110^\circ\); возьмите на соответствующем луче точку и соедините с другим концом основания. Такой треугольник всегда имеет высоты, две из которых падают вне треугольника. Учитывая сумму углов \(180^\circ\), два остальных угла будут острыми, так как их сумма равна \(180^\circ-110^\circ=70^\circ\).

г) Равносторонний: все стороны равны, следовательно, все углы равны по \(60^\circ\). Построение циркулем: проведите сторону длиной \(a\), из её концов постройте две окружности радиуса \(a\); их пересечение даёт третью вершину. Соедините вершины — получится треугольник с тремя равными сторонами и углами. Высоты, медианы, биссектрисы и средние линии совпадают и пересекаются в одной точке.

д) Равнобедренный: две стороны равны, а углы при основании равны. Возьмите основание длиной \(b\), постройте его середину и поднимите перпендикуляр; отметьте на нём точку на расстоянии \(h\) от основания и соедините с концами основания — получатся равные боковые стороны. В таком треугольнике медиана к основанию является также высотой и биссектрисой, а углы у основания равны, то есть \(\angle A=\angle B\).

е) Разносторонний: все три стороны попарно различны, следовательно, и углы попарно различны. Построить можно по трём произвольным отрезкам, удовлетворяющим неравенствам треугольника: для длин \(a,b,c\) должно выполняться \(a<b+c\), \(b<a+c\), \(c<a+b\). Например, возьмите основание \(a\), затем из его концов проведите окружности радиусов \(b\) и \(c\); их пересечение даст третью вершину. Ни одна осевая симметрия у такого треугольника отсутствует.

ж) Тупоугольный и равнобедренный: две стороны равны и один угол \(>90^\circ\). Удобно задать вершину при вершине равных боковых сторон так, чтобы угол при ней был тупым, например \(120^\circ\), и провести равные лучи; затем отметить точки на одинаковом расстоянии \(l\) и соединить с основанием. Тогда углы у основания равны и будут острыми, их сумма равна \(180^\circ-120^\circ=60^\circ\), то есть каждый по \(30^\circ\). Высота к основанию лежит на оси симметрии и выходит вне треугольника, если опускать её из тупого угла на продолжение основания.

з) Остроугольный и равнобедренный: две стороны равны, все углы \(<90^\circ\). Постройте равнобедренный треугольник с вершиной при малом угле, например \(\angle C=40^\circ\); тогда углы при основании равны по \(\frac{180^\circ-40^\circ}{2}=70^\circ\), оба острые. Осевая симметрия проходит через вершину и середину основания, эта же прямая является высотой, медианой и биссектрисой.

и) Прямоугольный и равнобедренный: один угол \(90^\circ\) и равные катеты. Постройте прямой угол, на его лучах отложите равные отрезки \(a\) и соедините их концы — получим равнобедренный прямоугольный треугольник, где катеты равны, а острые углы равны по \(45^\circ\), так как \(\frac{180^\circ-90^\circ}{2}=45^\circ\). Гипотенуза равна \(a\sqrt{2}\), а медиана к гипотенузе равна \(\frac{\sqrt{2}}{2}a\) и одновременно равна половине гипотенузы.