ГДЗ по Математике 6 Класс Часть 1 Номер 1.143 Виленкин, Жохов — Подробные Ответы

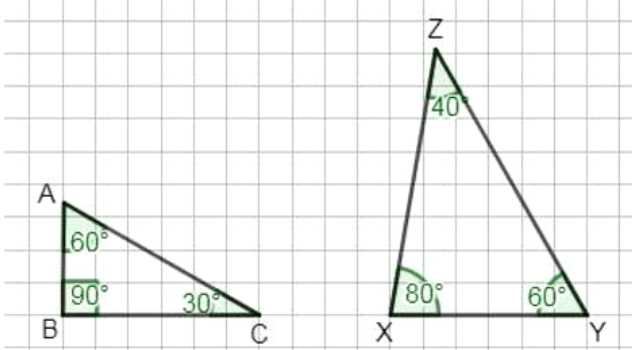
а) Начертите прямоугольный треугольник \(ABC\) и остроугольный треугольник \(XZY\). Измерьте транспортиром их углы. Найдите сумму углов в этих треугольниках.  

б) Какое предположение можно сделать из решения задач 1.142 и 1.143, а?

а) Измеряем углы: у \(ABC\) получаем \(60^\circ, 90^\circ, 30^\circ\). Складываем: \(60^\circ+90^\circ+30^\circ=180^\circ\). У \(XZY\) получаем \(80^\circ, 40^\circ, 60^\circ\). Складываем: \(80^\circ+40^\circ+60^\circ=180^\circ\).

б) Предположение: сумма внутренних углов любого треугольника равна \(180^\circ\).

а) Строим прямоугольный треугольник \(ABC\) с прямым углом при вершине \(B\), затем транспортиром последовательно измеряем каждый угол. Пусть измерения дают углы \( \angle A=60^\circ\), \( \angle B=90^\circ\), \( \angle C=30^\circ\). Складываем результаты измерений для проверки: \(60^\circ+90^\circ+30^\circ=180^\circ\). Аналогично строим остроугольный треугольник \(XZY\), у которого все углы острые, и измеряем транспортиром: пусть получены \( \angle X=80^\circ\), \( \angle Z=40^\circ\), \( \angle Y=60^\circ\). Проверяем сумму: \(80^\circ+40^\circ+60^\circ=180^\circ\). Оба случая показывают, что сумма внутренних углов на примерах даёт один и тот же результат.

а) При измерении важно следить за точной установкой центра транспортира на вершину угла и совмещением нулевой отметки со стороны угла, иначе возникает систематическая ошибка. Если после аккуратного измерения получаем, что у прямоугольного треугольника один угол равен \(90^\circ\), то сумма двух остальных по измерениям дополняет до \(180^\circ\), как видно из вычисления \(90^\circ+(60^\circ+30^\circ)=180^\circ\). В остроугольном треугольнике каждый из трёх углов меньше \(90^\circ\), но их сумма по измерениям также даёт \(180^\circ\), что подтверждается вычислением \(80^\circ+40^\circ+60^\circ=180^\circ\). Эти результаты согласуются между собой и не зависят от конкретных величин углов при условии корректного построения и измерения.

б) Предположение: на основании двух независимых измерительных проверок можно сформулировать обобщение, что сумма внутренних углов любого треугольника равна \(180^\circ\). То есть для произвольного треугольника \( \triangle ABC\) выполняется \( \angle A+\angle B+\angle C=180^\circ\). Этот вывод согласуется как с результатом для прямоугольного треугольника, где \( \angle B=90^\circ\) и тогда \( \angle A+\angle C=180^\circ-90^\circ=90^\circ\), так и для остроугольного треугольника, где каждая из величин меньше \(90^\circ\), но их сумма остаётся равной \(180^\circ\).