
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 1.142 Виленкин, Жохов — Подробные Ответы
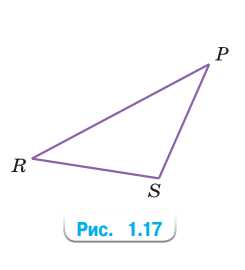
Измерьте углы треугольника \(PRS\) на рисунке 1.17. Найдите сумму углов треугольника.
Дано: \(\angle S=105^\circ\), \(\angle P=40^\circ\), \(\angle R=35^\circ\).
Сумма внутренних углов треугольника равна \(180^\circ\). Тогда \(\angle S+\angle P+\angle R=105^\circ+40^\circ+35^\circ=180^\circ\).
Ответ: \(180^\circ\).
1) Сначала фиксируем измеренные углы треугольника \(PRS\): по рисунку заданы величины \(\angle S=105^\circ\), \(\angle P=40^\circ\), \(\angle R=35^\circ\). Эти три угла являются тремя внутренними углами одного и того же треугольника, поэтому каждому соответствует единственная вершина треугольника \(S\), \(P\) и \(R\). Значения приведены в градусной мере, что позволяет напрямую использовать правило о сумме внутренних углов треугольника в евклидовой геометрии.
2) Ключевой факт: для любого треугольника сумма его внутренних углов постоянна и равна \(180^\circ\). Это следует из параллельных прямых и накрест лежащих углов или из аксиоматического свойства плоскости Евклида. Применяем этот факт к нашему треугольнику \(PRS\), где внутренние углы именно \(\angle S\), \(\angle P\) и \(\angle R\).
3) Складываем данные величины: \(\angle S+\angle P+\angle R=105^\circ+40^\circ+35^\circ\). Сначала суммируем два угла: \(105^\circ+40^\circ=145^\circ\). Затем добавляем третий угол: \(145^\circ+35^\circ=180^\circ\). Получившаяся сумма точно совпадает с теоретическим значением суммы внутренних углов треугольника, что дополнительно подтверждает корректность измерений.
Ответ: \(180^\circ\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!