ГДЗ по Математике 6 Класс Часть 1 Номер 1.137 Виленкин, Жохов — Подробные Ответы

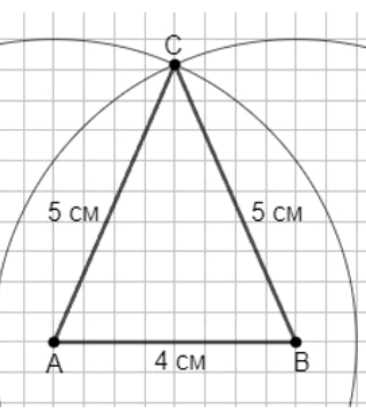
а) Постройте равнобедренный треугольник, у которого основание равно 4 см, а боковые стороны равны по 5 см.  

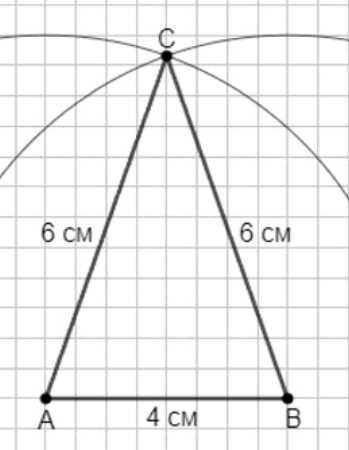
б) Постройте равнобедренный треугольник, у которого основание равно 4 см, а боковые стороны равны по 6 см.  

в) Можно ли построить равнобедренный треугольник, у которого основание равно 4 см, а боковые стороны равны по 2 см? Сделайте предположение: «Сумма любых двух сторон треугольника … третьей стороны».

а) Построение: на прямой отложить основание \(AB=4\) см. Построить окружности с центрами в \(A\) и \(B\) радиуса \(5\) см; их пересечение \(C\). Соединить \(C\) с \(A\) и \(B\). Получим равнобедренный треугольник \(ABC\) с \(AC=BC=5\) см.

б) Построение: на прямой отложить основание \(AB=4\) см. Построить окружности с центрами в \(A\) и \(B\) радиуса \(6\) см; их пересечение \(C\). Соединить \(C\) с \(A\) и \(B\). Получим \(AC=BC=6\) см.

в) Построить нельзя: при \(AB=4\) см и \(AC=BC=2\) см окружности радиуса \(2\) см с центрами в \(A\) и \(B\) касаются в середине \(AB\), точка пересечения лежит на основании, треугольник не образуется, так как \(2+2=4\), то есть сумма двух сторон не больше третьей. Следовательно, верное утверждение: «Сумма любых двух сторон треугольника больше третьей стороны», то есть \(a+b>c\), \(a+c>b\), \(b+c>a\).

а) Построение треугольника с основанием \(AB=4\) см и боковыми сторонами по \(5\) см выполняем по шагам. Сначала на линии нанесём отрезок \(AB\) длиной ровно \(4\) см, пользуясь линейкой и отметив точки \(A\) и \(B\). Далее берём циркуль, устанавливаем раствор ровно \(5\) см, это значение фиксирует будущие длины боковых сторон. Проводим окружность с центром в \(A\) и радиусом \(5\) см: любая её точка удалена от \(A\) именно на \(5\) см, значит будет удовлетворять условию \(AC=5\) см. Затем, не меняя раствора циркуля, строим окружность с центром в \(B\) и тем же радиусом \(5\) см: любая её точка удалена от \(B\) на \(5\) см, то есть удовлетворяет \(BC=5\) см. Две окружности пересекаются в одной или двух точках; выбираем верхнюю точку пересечения \(C\) для получения «остроконного» варианта. Соединяя \(C\) с \(A\) и \(B\), получаем треугольник \(ABC\), в котором по построению \(AC=5\) см и \(BC=5\) см, а основание \(AB=4\) см. Корректность проверяется правилом: точка \(C\) лежит на обеих окружностях, значит одновременно выполнены равенства \(AC=5\) и \(BC=5\); следовательно, треугольник равнобедренный с вершиной при \(C\), а его высота, медиана и биссектриса из \(C\) совпадают и падают на середину основания \(AB\).

б) Построение при основании \(AB=4\) см и боковых сторонах по \(6\) см аналогично, но с иным радиусом окружностей. Сначала откладываем отрезок \(AB=4\) см. Настраиваем циркуль на раствор \(6\) см. Проводим окружность с центром \(A\) радиуса \(6\) см и окружность с центром \(B\) того же радиуса. Их пересечения дают точки, одинаково удалённые от \(A\) и \(B\) на \(6\) см. Выбираем верхнюю точку \(C\) и соединяем её с \(A\) и \(B\). Получаем равнобедренный треугольник \(ABC\) с \(AC=BC=6\) см, \(AB=4\) см. Заметим, что при таком соотношении сторон высота из \(C\) больше, чем в пункте а), что геометрически отражается в большем расстоянии между дугами окружностей и основанием. Условие существования треугольника выполнено, так как \(6+6>4\), \(6+4>6\), \(6+4>6\).

в) Построение при основании \(AB=4\) см и боковых сторонах по \(2\) см невозможно. Если отложить \(AB=4\) см и провести окружности радиуса \(2\) см с центрами \(A\) и \(B\), то они соприкасаются в одной точке, лежащей ровно посередине основания \(AB\). Эта точка не даёт вершину треугольника, так как она лежит на прямой \(AB\) и приводит к вырождению фигуры в отрезок: получаем \(AC=2\), \(BC=2\) и одновременно \(AB=4\), при этом выполняется равенство \(2+2=4\), а не строгое неравенство. Следовательно, треугольник не существует, потому что для любых сторон \(a\), \(b\), \(c\) истинно строгое требование треугольника: \(a+b>c\), \(a+c>b\), \(b+c>a\). В рассматриваемом случае имеем нарушение строгой формы условия существования, равенство не допускается, поэтому множество допустимых вершин \(C\) вне прямой \(AB\) есть \(\emptyset\). Итоговое утверждение формулируется так: сумма любых двух сторон треугольника больше третьей стороны, то есть \(a+b>c\), \(b+c>a\), \(a+c>b\), и только при строгих неравенствах возможно построение невырожденного треугольника.