
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 1.136 Виленкин, Жохов — Подробные Ответы
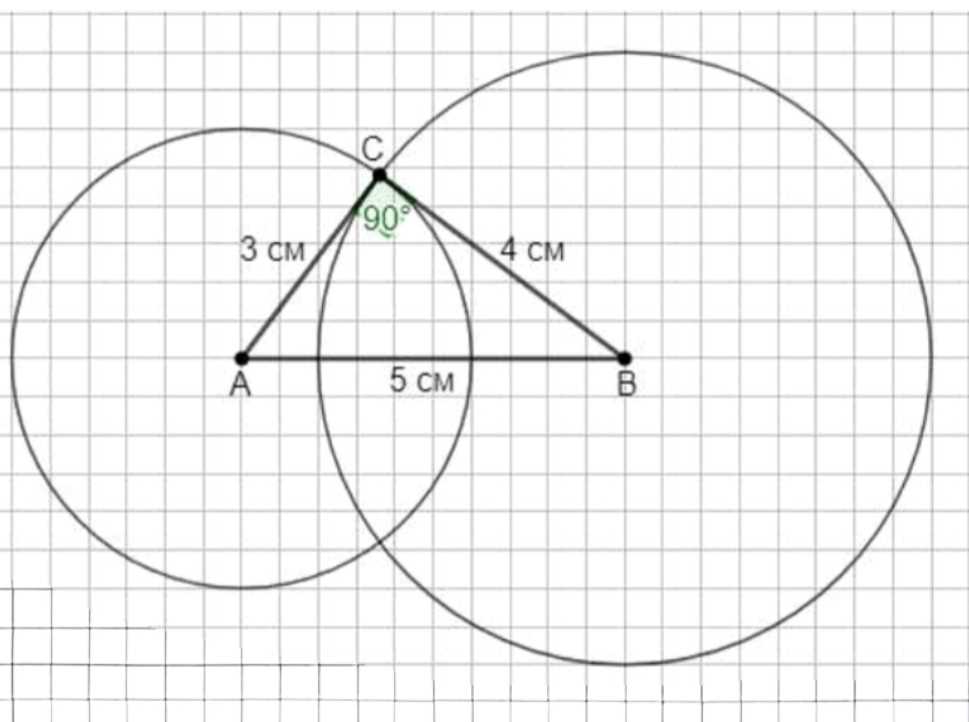
а) Используя линейку и циркуль, постройте по алгоритму треугольник \(ABC\), у которого сторона \(AB\) равна 5 см, сторона \(AC\) — 3 см и сторона \(BC\) — 4 см.
- Начертите отрезок \(AB\), равный 5 см.
- Проведите окружность с центром в точке \(A\) и радиусом 3 см.
- Проведите окружность с центром в точке \(B\) и радиусом 4 см.
- Обозначьте одну из точек пересечения окружностей буквой \(C\).
- Проведите отрезки \(AC\) и \(BC\).
б) Измерьте транспортиром угол \(C\) треугольника. Какой треугольник построен?
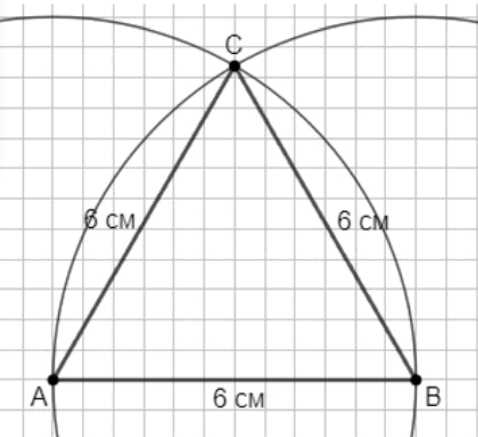
в) Используя линейку и циркуль, постройте по алгоритму равносторонний треугольник \(ABC\), сторона которого равна 6 см.
а) Строим: \(AB=5\) см; окружность с центром \(A\) радиуса \(3\) см; окружность с центром \(B\) радиуса \(4\) см; их пересечение даёт точку \(C\). Соединяем \(AC\) и \(BC\). По теореме Пифагора \(3^{2}+4^{2}=9+16=25=5^{2}\), значит \(\angle C=90^\circ\), все стороны совпадают с заданными, треугольник построен.
б) Так как \(AC^{2}+BC^{2}=AB^{2}\), то \(\angle C=90^\circ\). Построенный треугольник прямоугольный.
в) Равносторонний треугольник со стороной \(6\) см: строим отрезок \(AB=6\) см; окружности с центрами \(A\) и \(B\) радиуса \(6\) см; их пересечение — точка \(C\); соединяем \(AC\) и \(BC\). Тогда \(AB=BC=CA=6\) см, следовательно, \(\angle A=\angle B=\angle C=60^\circ\).
а) Пошаговое построение треугольника по длинам сторон: сначала откладываем на линейке отрезок \(AB=5\) см, обозначая его концы точками \(A\) и \(B\). Далее циркулем устанавливаем размах на \(3\) см и проводим окружность с центром в точке \(A\); множество её точек — это все точки, удалённые от \(A\) на \(3\) см, значит любая такая точка будет возможным положением вершины \(C\) при условии \(AC=3\) см. Затем, не меняя инструментов, выставляем размах циркуля на \(4\) см и чертим окружность с центром в точке \(B\); её точки — все возможные положения вершины \(C\) при условии \(BC=4\) см. Точки пересечения этих двух окружностей удовлетворяют одновременно условиям \(AC=3\) см и \(BC=4\) см. Выбираем одну из точек пересечения и обозначаем её \(C\). Соединяем \(A\) с \(C\) и \(B\) с \(C\), получая треугольник \(ABC\) с требуемыми длинами сторон \(AB=5\) см, \(AC=3\) см, \(BC=4\) см. Проверка корректности: так как построение использует окружности радиусов, равных заданным сторонам, то полученные отрезки автоматически имеют нужные длины; отличаться они не могут, поскольку каждая окружность задаёт строго фиксированное расстояние до своего центра.
б) Обоснование вида треугольника и измерение угла при вершине \(C\): по соотношению длин сторон имеем \(AC=3\) см, \(BC=4\) см, \(AB=5\) см. Проверим теорему Пифагора: \(AC^{2}+BC^{2}=3^{2}+4^{2}=9+16=25=5^{2}=AB^{2}\). Равенство \(AC^{2}+BC^{2}=AB^{2}\) выполняется, следовательно, угол при вершине \(C\) является прямым, то есть \(\angle C=90^\circ\). Это утверждение не зависит от конкретного расположения треугольника на плоскости и является следствием обратной теоремы Пифагора: если для трёх положительных чисел, интерпретируемых как длины сторон треугольника, выполняется равенство \(a^{2}+b^{2}=c^{2}\), где \(c\) — наибольшая сторона, то угол, лежащий напротив стороны длины \(c\), прямой. Дополнительно можно провести практическую проверку транспортиром: приложить центр транспортира к точке \(C\), совместить его нулевую отметку с одним из лучей угла \(CA\) или \(CB\) и убедиться, что второй луч показывает \(90^\circ\), что согласуется с расчетом по теореме Пифагора.
в) Построение равностороннего треугольника со стороной \(6\) см линейкой и циркулем: откладываем отрезок \(AB=6\) см. Устанавливаем циркуль на размах \(6\) см и проводим окружность с центром \(A\); любая точка на этой окружности находится на расстоянии \(6\) см от \(A\), то есть будет удовлетворять условию \(AC=6\) см. Не меняя размаха, проводим окружность с центром \(B\); точки этой окружности удовлетворяют условию \(BC=6\) см. Точки пересечения окружностей дают возможные вершины \(C\), для которых одновременно выполняются равенства \(AC=6\) см и \(BC=6\) см. Выбираем одну из точек пересечения и обозначаем её \(C\). Соединяем \(A\) с \(C\) и \(B\) с \(C\). Получаем треугольник, в котором \(AB=BC=CA=6\) см. Так как во всяком равностороннем треугольнике все стороны равны, то и все углы равны: \(\angle A=\angle B=\angle C=60^\circ\). Правильность гарантируется свойством окружностей одинакового радиуса: их пересечение приводит к треугольнику с тремя равными сторонами, поскольку каждая вершина \(C\) выбранна так, чтобы одновременно сохранялись расстояния \(AC=6\) см и \(BC=6\) см, а исходный отрезок \(AB\) также равен \(6\) см.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!