ГДЗ по Математике 6 Класс Часть 1 Номер 1.135 Виленкин, Жохов — Подробные Ответы

Используя линейку и транспортир, постройте треугольник \(ABC\), у которого:  

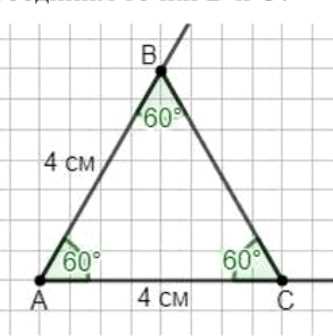
а) угол \(A\) равен 60°, а стороны \(AB\) и \(AC\) равны по 4 см;  

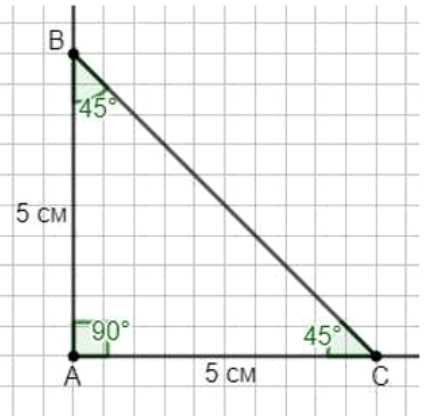
б) угол \(A\) прямой, а стороны \(AB\) и \(AC\) равны по 5 см;  

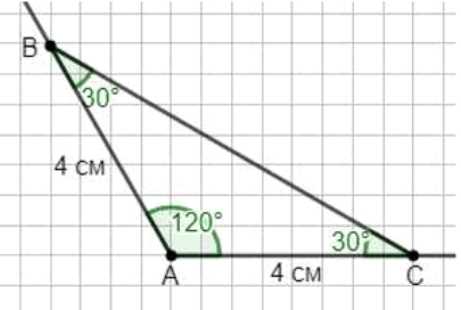
в) угол \(A\) равен 120°, а стороны \(AB\) и \(AC\) равны по 4 см. Какой треугольник построен? Измерьте транспортиром его углы \(B\) и \(C\). Какое можно сделать предположение об углах при основании равнобедренного треугольника?

а) Строим угол \(A=60^\circ\). На его сторонах откладываем \(AB=AC=4\) см, соединяем \(B\) и \(C\). Получился равнобедренный, а по измерению равносторонний треугольник: \(\angle B=\angle C=60^\circ\).

б) Строим прямой угол \(A=90^\circ\). На сторонах откладываем \(AB=AC=5\) см, соединяем \(B\) и \(C\). Получился равнобедренный прямоугольный треугольник: \(\angle B=\angle C=45^\circ\).

в) Строим угол \(A=120^\circ\). На его сторонах откладываем \(AB=AC=4\) см, соединяем \(B\) и \(C\). Получился равнобедренный треугольник: \(\angle B=\angle C=30^\circ\).

Предположение: в равнобедренном треугольнике углы при основании равны.

а) Построение: приложите транспортир к точке \(A\) и отметьте лучи, образующие угол \(A=60^\circ\). По линейке отложите на каждом луче отрезки одинаковой длины \(AB=4\) см и \(AC=4\) см. Соедините полученные точки \(B\) и \(C\). Получаем равнобедренный треугольник с вершиной при \(A\). Поскольку две стороны равны, углы при основании равны: \(\angle B=\angle C\). Измерением транспортиром убеждаемся, что сумма углов треугольника равна \(180^\circ\): \(\angle A+\angle B+\angle C=180^\circ\). Так как \(\angle A=60^\circ\) и \(\angle B=\angle C\), то \(60^\circ+2\angle B=180^\circ\), откуда \(\angle B=\angle C=60^\circ\); следовательно, фактически построен равносторонний треугольник со сторонами \(AB=BC=CA=4\) см и равными углами по \(60^\circ\). Измерение подтверждает вычисление.

б) Построение: постройте прямой угол в точке \(A\), то есть \(\angle A=90^\circ\), и отложите по его сторонам равные отрезки \(AB=AC=5\) см. Соедините \(B\) и \(C\). Получился равнобедренный прямоугольный треугольник. По равенству боковых сторон имеем \(\angle B=\angle C\). Используем сумму углов треугольника: \(\angle A+\angle B+\angle C=180^\circ\). Так как \(\angle A=90^\circ\) и \(\angle B=\angle C\), получаем \(90^\circ+2\angle B=180^\circ\), следовательно \(\angle B=\angle C=45^\circ\). Измерение транспортиром фиксирует половину прямого угла у основания, что согласуется с расчетом. Длина гипотенузы при желании проверяется по теореме Пифагора: \(BC=\sqrt{AB^{2}+AC^{2}}=\sqrt{5^{2}+5^{2}}=\sqrt{50}=5\sqrt{2}\) см.

в) Построение: постройте в точке \(A\) тупой угол \(\angle A=120^\circ\). На его сторонах отложите равные отрезки \(AB=AC=4\) см и соедините точки \(B\) и \(C\). Получился равнобедренный треугольник с боковыми сторонами по 4 см. По свойству равнобедренного треугольника \(\angle B=\angle C\). Применяем сумму углов: \(\angle A+\angle B+\angle C=180^\circ\). Подставляя \(\angle A=120^\circ\) и равенство базовых углов, имеем \(120^\circ+2\angle B=180^\circ\), откуда \(\angle B=\angle C=30^\circ\). Измерение транспортиром подтверждает, что каждый из углов при основании составляет треть развёрнутого угла после вычитания вершины.

Вывод и предположение: во всех трёх случаях строились треугольники с равными боковыми сторонами \(AB=AC\), то есть равнобедренные. Из равенства сторон следует равенство углов при основании: \(\angle B=\angle C\). Проверка суммой углов треугольника в каждом примере даёт одинаковый результат: при заданном \(\angle A\) базовые углы вычисляются по формуле \(\angle B=\angle C=\frac{180^\circ-\angle A}{2}\). Следовательно, можно сформулировать общее утверждение: в любом равнобедренном треугольнике углы при основании равны, а их величина равна половине разности между \(180^\circ\) и углом при вершине.