
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 1.134 Виленкин, Жохов — Подробные Ответы
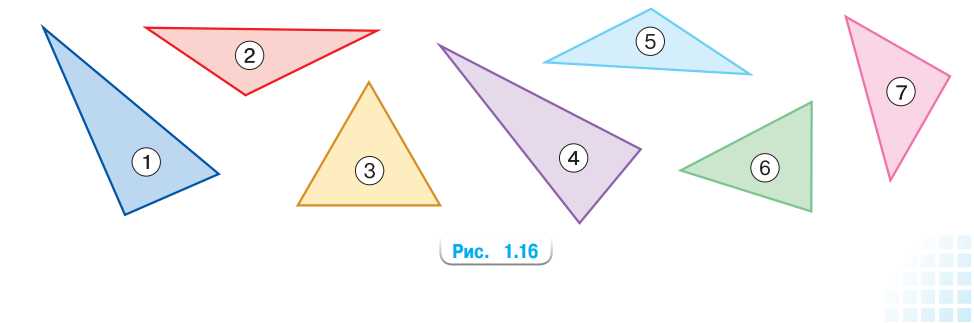
На рисунке 1.16 изображены треугольники.
а) Используя чертёжный треугольник, определите и запишите виды треугольников по углам.
б) Используя линейку, определите и запишите виды треугольников по сторонам.
в) По результатам, полученным в пунктах а) и б), заполните таблицу на с. 34.
а) По углам: остроугольные — 3, 4, 6; прямоугольные — 1, 7; тупоугольные — 2, 5. Проверка: у прямоугольных один угол равен \(90^\circ\), у тупоугольных один угол больше \(90^\circ\), у остроугольных все углы меньше \(90^\circ\).
б) По сторонам: равносторонний — 3; равнобедренные — 4, 5, 7; разносторонние — 1, 2, 6. Проверка линейкой: у равностороннего все три стороны равны, у равнобедренных две стороны равны, у разносторонних все стороны различны.
в) Таблица:
| Углы \\ Стороны | Разносторонний | Равнобедренный | Равносторонний |
|---|---|---|---|
| Прямоугольный | 1 | 7 | \(\emptyset\) |
| Тупоугольный | 2 | 5 | \(\emptyset\) |
| Остроугольный | 6 | 4 | 3 |
а) Классификация по углам выполняется по признакам величин углов. Прямоугольный треугольник имеет один угол ровно \(90^\circ\): на рисунке это №1 и №7, что видно по явной вершине с перпендикулярными сторонами. Тупоугольный треугольник имеет один угол больше \(90^\circ\): это №2 и №5, у них одна вершина «раскрыта» шире прямого угла. Остроугольный треугольник имеет три острых угла (каждый меньше \(90^\circ\)): это №3, №4 и №6, у них все вершины острые, без прямого или тупого угла. При проверке чертёжным треугольником совмещаем катеты с двумя сторонами угла: если совпадение точное — угол \(90^\circ\) (прямоугольный), если угол шире — \(>90^\circ\) (тупоугольный), если уже — \(<90^\circ\) (остроугольный). б) Классификация по сторонам основана на сравнении длин линейкой. Равносторонний треугольник имеет три равные стороны: №3 (все три измерения совпадают), у него также три равных угла по \(60^\circ\), что согласуется с видом по углам. Равнобедренный имеет ровно две равные стороны: №4, №5, №7; при измерении получаем пары равных отрезков, а углы при основании равны. Разносторонний имеет три различные стороны: №1, №2, №6; линейка показывает, что ни одна пара сторон не равна. Напомним: для любых трёх сторон выполняется неравенство треугольника \(a+b>c\), \(a+c>b\), \(b+c>a\); визуально эти условия соблюдены у всех фигур.
в) Сведение результатов в таблицу позволяет увидеть сочетания «углы × стороны». Прямоугольный треугольник не может быть равносторонним, так как в равностороннем все углы равны \(60^\circ\), следовательно, в строке «прямоугольный» допустимы только разносторонний и равнобедренный варианты (в нашем наборе это №1 и №7). Тупоугольный также не может быть равносторонним, поскольку равносторонний имеет одинаковые углы \(60^\circ\), а тупой угол \(>90^\circ\); потому в строке «тупоугольный» остаются разносторонний и равнобедренный (№2 и №5). Остроугольный может быть как разносторонним, так и равнобедренным, и равносторонним: в наборе присутствуют все три случая — №6 (разносторонний остроугольный), №4 (равнобедренный остроугольный), №3 (равносторонний остроугольный). Итоговые позиции идентичны результатам измерений и визуальной верификации углов.
- По углам: остроугольные — 3, 4, 6; прямоугольные — 1, 7; тупоугольные — 2, 5.
- По сторонам: равносторонний — 3; равнобедренные — 4, 5, 7; разносторонние — 1, 2, 6.
- Таблица:
Углы \\ Стороны Разносторонний Равнобедренный Равносторонний Прямоугольный 1 7 \(\emptyset\) Тупоугольный 2 5 \(\emptyset\) Остроугольный 6 4 3

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!