ГДЗ по Математике 6 Класс Часть 1 Номер 1.122 Виленкин, Жохов — Подробные Ответы

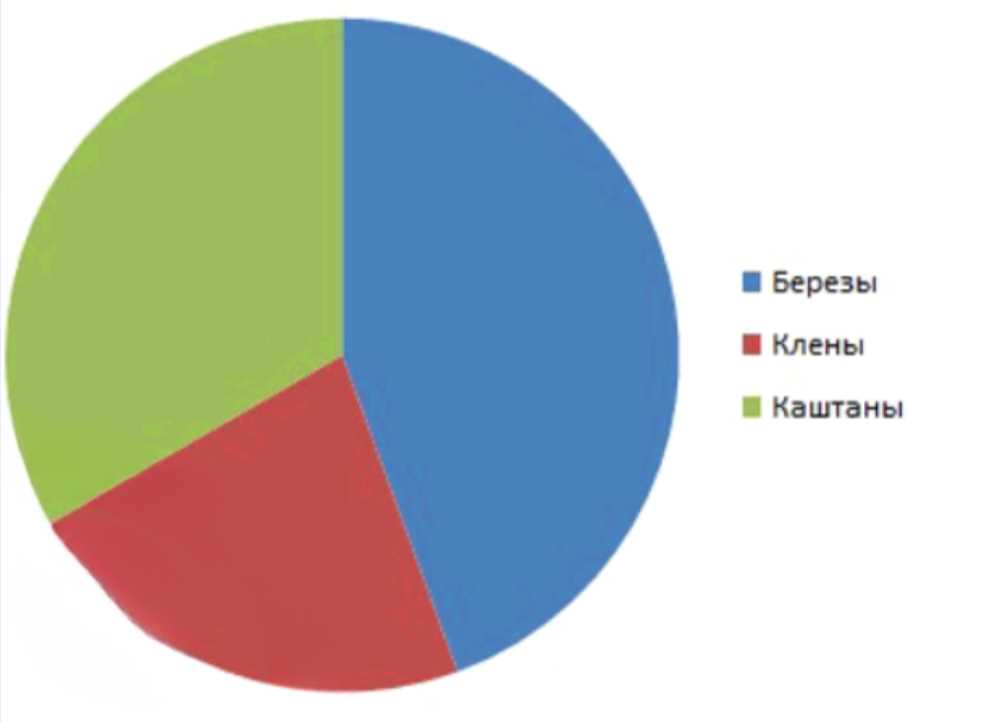
Вокруг школы посадили 36 деревьев: 16 берёз, 8 клёнов, а остальные — каштаны. Изобразите в круговой диаграмме видовой состав деревьев.

Всего деревьев \(36\). На один объект в круге приходится \(360:36=10^\circ\).

Берёзы: \(16\cdot10^\circ=160^\circ\).

Клёны: \(8\cdot10^\circ=80^\circ\).

Каштаны: \((36-16-8)\cdot10^\circ=12\cdot10^\circ=120^\circ\).

Итог для круговой диаграммы: берёзы — \(160^\circ\), клёны — \(80^\circ\), каштаны — \(120^\circ\).

1) Имеется общий круг диаграммы, который всегда равен полному углу \(360^\circ\). Всего посажено \(36\) деревьев, значит один сектор, соответствующий одному дереву, должен занимать равную долю полного круга. Находим угловую меру, приходящуюся на одно дерево: \(360:36=10^\circ\). Это базовый шаг: сначала нормируем данные к «цене деления» в градусах, чтобы затем умножать на количество деревьев каждого вида и получать углы секторов.

2) Для берёз известно количество \(16\). Угол сектора равен числу объектов, умноженному на угловую меру одного объекта: \(16\cdot10^\circ=160^\circ\). Это означает, что почти половина круга (чуть меньше, чем полукруг \(180^\circ\)) будет занята сектором берёз. При построении диаграммы удобно отложить сначала крупный сектор, чтобы визуально контролировать сумму углов.

3) Для клёнов известно количество \(8\). Аналогично вычисляем угол: \(8\cdot10^\circ=80^\circ\). Этот сектор заметно меньше сектора берёз и составляет чуть меньше четверти круга, так как четверть равна \(90^\circ\). Размещение второго сектора выполняется смежно к первому, не меняя общей ориентации диаграммы.

4) Число каштанов сначала находим как остаток от общего количества: \(36-16-8=12\) деревьев. Переводим в угол: \((36-16-8)\cdot10^\circ=12\cdot10^\circ=120^\circ\). Этот сектор равен ровно трети круга, так как треть круга это \(360^\circ\cdot\frac{1}{3}=120^\circ\). Для проверки корректности складываем все полученные углы: \(160^\circ+80^\circ+120^\circ=360^\circ\), что подтверждает полноту распределения без пропусков и перекрытий.

5) Итоговые значения для круговой диаграммы: берёзы — \(160^\circ\), клёны — \(80^\circ\), каштаны — \(120^\circ\). При построении: нарисуйте окружность, выберите начальный луч, отложите последовательно углы \(160^\circ\), затем \(80^\circ\), оставшийся сектор автоматически составит \(120^\circ\). Подпишите сектора и при желании используйте разные цвета: берёзы — синий, клёны — красный, каштаны — зелёный; доли соответствуют отношениям \( \frac{16}{36}=\frac{4}{9}\), \( \frac{8}{36}=\frac{2}{9}\), \( \frac{12}{36}=\frac{1}{3}\), что согласуется с углами \(160^\circ\), \(80^\circ\) и \(120^\circ\).