
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 1.116 Виленкин, Жохов — Подробные Ответы
Постройте развёрнутый угол \(ROT\) и проведите луч \(OS\). Чему равны углы \(POS\) и \(SOT\), если:
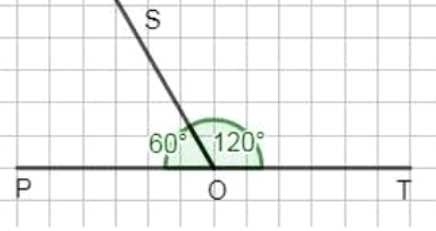
а) угол \(POS\) вдвое меньше угла \(SOT\);
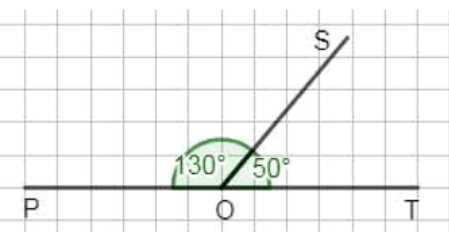
б) угол \(POS\) на 80° больше угла \(SOT\);
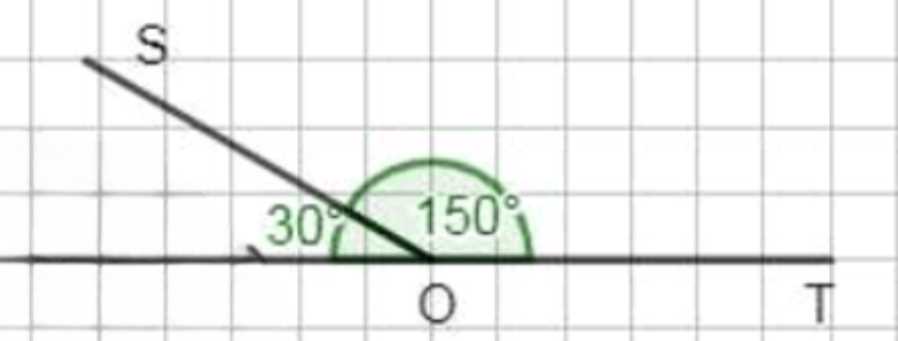
в) угол \(SOT\) в 5 раз больше угла \(POS\)?
а) Пусть \( \angle POS = x^\circ\), тогда \( \angle SOT = 2x^\circ\). На развернутом угле \(ROT\): \(x+2x=180^\circ \Rightarrow 3x=180^\circ \Rightarrow x=60^\circ\). Значит, \( \angle POS=60^\circ\), \( \angle SOT=120^\circ\).
б) Пусть \( \angle POS = x^\circ\), тогда \( \angle SOT = x-80^\circ\). Имеем \(x+(x-80)=180^\circ \Rightarrow 2x=260^\circ \Rightarrow x=130^\circ\). Значит, \( \angle POS=130^\circ\), \( \angle SOT=50^\circ\).
в) Пусть \( \angle POS = x^\circ\), тогда \( \angle SOT = 5x^\circ\). Тогда \(x+5x=180^\circ \Rightarrow 6x=180^\circ \Rightarrow x=30^\circ\). Значит, \( \angle POS=30^\circ\), \( \angle SOT=150^\circ\).
а) На развернутом угле \(ROT\) сумма смежных углов вдоль прямой равна \(180^\circ\). По условию угол \(POS\) вдвое меньше угла \(SOT\), поэтому обозначим \( \angle POS = x^\circ\), тогда \( \angle SOT = 2x^\circ\). Складываем углы на прямой: \(x + 2x = 180^\circ\). Получаем уравнение \(3x = 180^\circ\), откуда \(x = 60^\circ\). Следовательно, \( \angle POS = 60^\circ\). Подставляя \(x\) во второе выражение, имеем \( \angle SOT = 2 \cdot 60^\circ = 120^\circ\). Эти значения согласуются с чертежом: меньший угол у точки \(O\) равен \(60^\circ\), а смежный к нему дополняет до прямой и потому равен \(120^\circ\).
б) Снова используем свойство развернутого угла: сумма смежных углов равна \(180^\circ\). По условию \( \angle POS\) на \(80^\circ\) больше, чем \( \angle SOT\). Обозначим \( \angle POS = x^\circ\), тогда \( \angle SOT = x — 80^\circ\). Складываем: \(x + (x — 80^\circ) = 180^\circ\). Преобразуем уравнение: \(2x — 80^\circ = 180^\circ\), откуда \(2x = 260^\circ\) и \(x = 130^\circ\). Значит, \( \angle POS = 130^\circ\). Тогда \( \angle SOT = 130^\circ — 80^\circ = 50^\circ\). Проверка: \(130^\circ + 50^\circ = 180^\circ\), что верно, следовательно, найденные значения корректны и соответствуют рисунку.
в) Здесь по условию угол \(SOT\) в \(5\) раз больше угла \(POS\). Пусть \( \angle POS = x^\circ\), тогда \( \angle SOT = 5x^\circ\). Так как это смежные углы на развернутом угле, имеем \(x + 5x = 180^\circ\). Отсюда \(6x = 180^\circ\), следовательно, \(x = 30^\circ\). Тогда \( \angle POS = 30^\circ\), а \( \angle SOT = 5 \cdot 30^\circ = 150^\circ\). Итоговые значения также удовлетворяют основному свойству: \(30^\circ + 150^\circ = 180^\circ\), что подтверждает правильность решения во всех трех пунктах.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!