ГДЗ по Математике 6 Класс Часть 1 Номер 1.115 Виленкин, Жохов — Подробные Ответы

Практическая работа  

Оборудование: циркуль, линейка, карандаш, транспортир.  

Порядок работы:  

1) Проведите окружность с центром \(O\) и её диаметр \(CD\).  

2) Используя транспортир, разделите оба развёрнутых угла \(COD\) на три равных угла. Отметьте точки пересечения сторон углов с окружностью буквами \(C, A, B, D, M\) и \(N\). Сколько получилось равных частей в круге?  

3) Соедините отрезками точки \(C, A, B, D, M\) и \(N\). Как называется этот многоугольник?  

4) Сравните стороны многоугольника и радиус круга. Сделайте предположение.

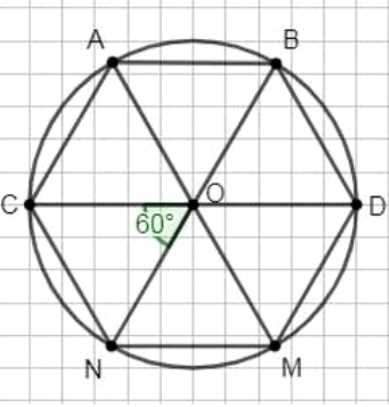
1) Разделили развёрнутый угол \(COD\) на три части: каждый угол равен \( \frac{180}{3}=60^\circ\). На окружности получилось шесть равных дуг, значит круг разбит на 6 равных частей.

2) Соединили точки \(C,A,B,D,M,N\): получился правильный шестиугольник \(CABDMN\).

3) Так как центральные углы по \(60^\circ\), то каждый треугольник с вершиной в центре равносторонний, следовательно, стороны шестиугольника равны между собой и равны радиусу: \(CA=AB=BD=DM=MN=NC=R\).

1) Построили окружность с центром \(O\) и диаметром \(CD\). Развёрнутый угол на прямой \(CD\) равен \(180^\circ\). Делим этот угол транспортиром на три равные части, поэтому каждая часть составляет \( \frac{180}{3}=60^\circ\). Такие же три части получаются и для второго развёрнутого угла на той же прямой, итого шесть центральных углов по \(60^\circ\). Лучи этих углов пересекают окружность в шести точках \(C,A,B,D,M,N\). Так как центральные углы равны, то соответствующие дуги равны; окружность разбита на шесть равных дуг, а круг — на шесть равных секторов.

2) Соединяем последовательно точки \(C,A,B,D,M,N\) хордами. Любые две соседние точки ограничивают дугу в \(60^\circ\), значит соответствующая хорда стягивает центральный угол \(60^\circ\). В каждом секторе получаем треугольник с вершиной в центре: например, \(\triangle COA\), \(\triangle AOB\) и т.д. В каждом таком треугольнике две стороны являются радиусами окружности, то есть равны \(R\), а угол между ними равен \(60^\circ\). Следовательно, каждый из этих треугольников равносторонний: если в треугольнике две стороны \(R\) и угол между ними \(60^\circ\), то третья сторона также равна \(R\), поскольку по свойству треугольника с углом \(60^\circ\) при равных прилежащих сторонах он становится равносторонним.

3) Отсюда длины всех хорд между соседними отмеченными точками одинаковы: \(CA=AB=BD=DM=MN=NC=R\). Таким образом, многоугольник \(CABDMN\), образованный этими хордами, имеет шесть равных сторон и шесть равных центральных углов, опирающихся на равные дуги, следовательно, он правильный. Название такого многоугольника — правильный шестиугольник. Итог: круг разделён на шесть равных частей, полученная фигура при соединении точек — правильный шестиугольник, причём каждая его сторона равна радиусу окружности: \( \text{сторона} = R\).