ГДЗ по Математике 6 Класс Часть 1 Номер 1.114 Виленкин, Жохов — Подробные Ответы

Практическая работа  

Оборудование: линейка, карандаш, циркуль, транспортир.  

Порядок работы:  

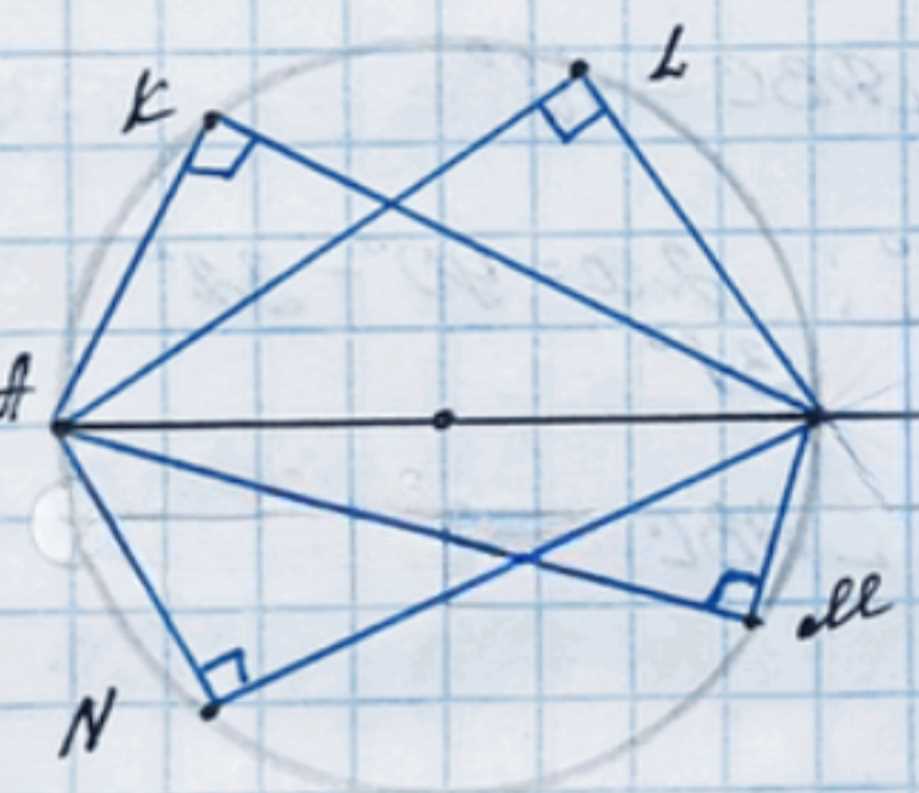
1) Проведите окружность и её диаметр \(AB\).  

2) На окружности отметьте точки \(K, L, M\) и \(N\).  

3) Соедините точки \(K, L, M\) и \(N\) с точками \(A\) и \(B\).  

4) Измерьте углы \(AKB, ALB, AMB\) и \(ANB\). Сделайте предположение о величине этих углов.  

5) Ответьте на вопрос: «Как построить прямой угол, имея только линейку и циркуль?»

Углы вписанные, опирающиеся на диаметр \(AB\), прямые: измерение показывает \( \angle AKB=90^\circ,\ \angle ALB=90^\circ,\ \angle AMB=90^\circ,\ \angle ANB=90^\circ\). Причина: вписанный угол, опирающийся на диаметр, равен половине центрального угла \(AOB=180^\circ\), значит \(90^\circ\).

Построение прямого угла линейкой и циркулем: построить окружность, провести её диаметр \(AB\); взять любую точку \(K\) на окружности, отличную от \(A\) и \(B\); соединить \(K\) с \(A\) и \(B\). Угол \( \angle AKB \) будет прямым.

1) На плоскости строим окружность произвольного радиуса с центром \(O\) и проводим ее диаметр \(AB\). Диаметр по определению проходит через центр, поэтому центральный угол \(AOB\) является развернутым: \( \angle AOB = 180^\circ \). Далее на окружности выбираем любые четыре точки \(K, L, M, N\), отличные от \(A\) и \(B\). Соединяем каждую из этих точек с концами диаметра отрезками \(AK, BK; AL, BL; AM, BM; AN, BN\). Получаем четыре вписанных угла, опирающихся на одну и ту же дугу \(AB\) полукруга.

2) По теореме о вписанном угле: величина любого вписанного угла равна половине величины соответствующего центрального угла, опирающегося на ту же дугу. Поскольку наши вписанные углы опираются на диаметр, им соответствует центральный угол \( \angle AOB = 180^\circ \). Следовательно, \( \angle AKB = \frac{1}{2}\cdot 180^\circ = 90^\circ \), аналогично \( \angle ALB = 90^\circ \), \( \angle AMB = 90^\circ \), \( \angle ANB = 90^\circ \). Это означает, что все такие углы прямые, независимо от выбора точки на окружности, и экспериментальное измерение транспортиром подтвердит одинаковый результат в пределах погрешности.

3) Причинно-следственная связь такова: дуга полукруга фиксирована, а любая точка \(X\) на этой дуге задает вписанный угол \( \angle AXB \). Поскольку длина дуги и центральный угол не меняются, величина вписанного угла остается постоянной. Геометрически это видно и через теорему о прямом угле в полукруге: треугольник \(AXB\) вписан в окружность, а сторона \(AB\) является диаметром, значит угол при вершине \(X\) прямой. Также можно увидеть через векторы или через скалярное произведение радиусов \(OA\) и \(OB\): \( \overrightarrow{OA} \) и \( \overrightarrow{OB} \) коллинеарны и направлены в противоположные стороны, что задает развернутый угол, а половина развернутого дает прямой.

4) Способ построить прямой угол, имея только линейку и циркуль: провести произвольный отрезок \(AB\); построить окружность с центром в середине этого отрезка. Для этого циркулем отмечают равные дуги из точек \(A\) и \(B\), получают пересечения, соединяют их и находят середину \(AB\) как пересечение серединного перпендикуляра с отрезком. С центром в найденной середине проводят окружность радиуса \(OA=\frac{1}{2}\cdot AB\); выбирают на окружности любую точку \(K\neq A,B\); соединяют \(K\) с \(A\) и \(B\). Тогда \( \angle AKB = 90^\circ \). Если требуется построить сам перпендикуляр к заданному лучу в точке, проводят диаметр через эту точку как через один конец хорды и берут вторую вершину на окружности: полученный угол при вершине на окружности будет прямой.

5) Итог измерений и теоретического обоснования: \( \angle AKB=90^\circ,\ \angle ALB=90^\circ,\ \angle AMB=90^\circ,\ \angle ANB=90^\circ \). Причина едина для всех случаев: каждый вписанный угол, опирающийся на диаметр, равен половине развернутого угла, то есть прямой. Поэтому диаграмма результатов измерений и вычисления совпадают, а указанный способ с диаметром дает чистое построение прямого угла только циркулем и линейкой.