ГДЗ по Математике 6 Класс Часть 1 Номер 1.112 Виленкин, Жохов — Подробные Ответы

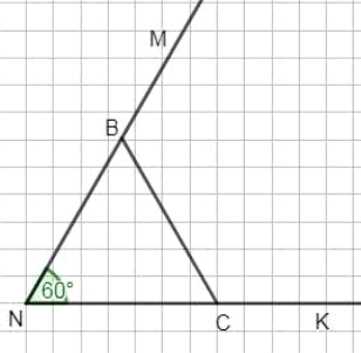
а) Постройте угол \(MNK\), градусная мера которого равна 60°. На сторонах угла отложите равные отрезки \(NB\) и \(NC\) и соедините отрезком точки \(B\) и \(C\).  

б) Измерьте стороны и углы треугольника \(CNB\) и сравните его стороны и углы.  

в) Найдите сумму углов и периметр треугольника наиболее удобным способом.

а) Строим угол \(MNK=60^\circ\). На сторонах откладываем равные отрезки \(NB=NC=3{,}5\ \text{см}\). Соединяем точки \(B\) и \(C\).

б) Так как лучи образуют \(60^\circ\) и точки \(B\) и \(C\) взяты на равных расстояниях от вершины \(N\), треугольник \(CNB\) равнобедренный и даже равносторонний: \(NB=NC=BC=3{,}5\ \text{см}\), углы равны \( \angle N=\angle B=\angle C=60^\circ\).

в) Сумма углов треугольника: \(60^\circ+60^\circ+60^\circ=180^\circ\).
Периметр: \(P=NB+NC+BC=3{,}5+3{,}5+3{,}5=10{,}5\ \text{см}\).

а) Строим угол с вершиной \(N\) так, чтобы его стороны были лучи \(NM\) и \(NK\), а градусная мера угла равнялась \(60^\circ\): \(\angle MNK=60^\circ\). На луче \(NM\) от точки \(N\) откладываем отрезок фиксированной длины, обозначим его \(NB\). На луче \(NK\) откладываем от точки \(N\) отрезок той же длины \(NC\), причём \(NB=NC\). Затем соединяем точки \(B\) и \(C\) прямым отрезком \(BC\). Благодаря симметрии относительно биссектрисы угла \(MNK\) (она проходит через \(N\) и делит угол \(60^\circ\) на два угла по \(30^\circ\)), точки \(B\) и \(C\) лежат на равных расстояниях от вершины \(N\) по разным сторонам, что создаёт в треугольнике \(CNB\) два равных ребра, исходящих из вершины \(N\).

б) Так как по условию отрезки откладывались равными, получаем равенство сторон \(NB=NC\), следовательно, треугольник \(CNB\) как минимум равнобедренный с основанием \(BC\). Кроме того, угол при вершине \(N\) равен углу исходного построения: \(\angle CNB=\angle MNK=60^\circ\). В равнобедренном треугольнике с вершиной при \(N\) и углом \(60^\circ\) при этой вершине сумма двух основанных углов равна \(180^\circ-60^\circ=120^\circ\), и по свойству равнобедренного треугольника они равны между собой: \(\angle C=\angle B=\frac{120^\circ}{2}=60^\circ\). Итак, все три угла равны \(60^\circ\), значит треугольник \(CNB\) равносторонний: \(NB=NC=BC\). Если по рисунку измерение даёт \(NB=NC=3{,}5\ \text{см}\), то из равносторонности следует \(BC=3{,}5\ \text{см}\). Углы сравниваются так: \(\angle N=\angle B=\angle C=60^\circ\); стороны сравниваются так: \(NB=NC=BC\).

в) Сумма углов любого треугольника равна \(180^\circ\). В нашем случае это наглядно подтверждается равенством углов: \(\angle N+\angle B+\angle C=60^\circ+60^\circ+60^\circ=180^\circ\). Периметр равностороннего треугольника равен утроенной длине его стороны. Так как каждая сторона равна \(3{,}5\ \text{см}\), получаем \(P=NB+NC+BC=3{,}5+3{,}5+3{,}5=10{,}5\ \text{см}\). Если требуется записать по формуле равностороннего треугольника, то \(P=3\cdot a\), где \(a=3{,}5\ \text{см}\), откуда \(P=3\cdot 3{,}5=10{,}5\ \text{см}\).