ГДЗ по Математике 6 Класс Часть 1 Номер 1.111 Виленкин, Жохов — Подробные Ответы

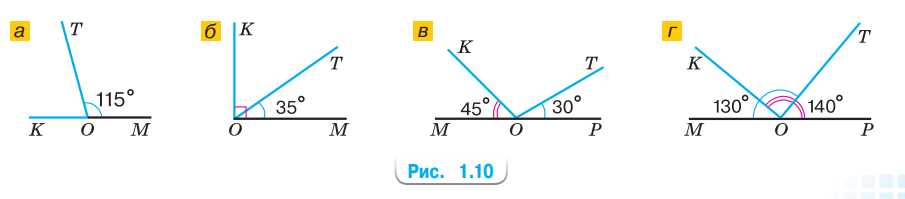
Найдите градусную меру угла \(KOT\) на рисунке 1.10.

а) Даны: \( \angle KOM=180^\circ\), \( \angle TOM=115^\circ\). Тогда смежные лучи дают \( \angle KOT=\angle KOM-\angle TOM=180^\circ-115^\circ=65^\circ\).

б) Даны: \( \angle KOM=90^\circ\), \( \angle TOM=35^\circ\). Тогда \( \angle KOT=\angle KOM-\angle TOM=90^\circ-35^\circ=55^\circ\).

в) Даны: \( \angle MOP=180^\circ\), \( \angle KOM=45^\circ\), \( \angle TOP=30^\circ\). Поскольку \( \angle KOM\) и \( \angle TOP\) входят в развернутый \( \angle MOP\), то \( \angle KOT=\angle MOP-(\angle KOM+\angle TOP)=180^\circ-(45^\circ+30^\circ)=105^\circ\).

г) Даны: \( \angle MOP=180^\circ\), \( \angle TOM=130^\circ\), \( \angle KOP=140^\circ\). Тогда \( \angle TOP=\angle MOP-\angle TOM=180^\circ-130^\circ=50^\circ\), \( \angle KOM=\angle MOP-\angle KOP=180^\circ-140^\circ=40^\circ\). Следовательно, \( \angle KOT=\angle MOP-(\angle KOM+\angle TOP)=180^\circ-(40^\circ+50^\circ)=90^\circ\).

а) Рассматриваем развернутый угол с вершиной в точке \(O\): \( \angle KOM=180^\circ\). Луч \(OT\) делит этот развернутый угол, образуя угол \( \angle TOM=115^\circ\). Так как развернутый угол равен сумме смежных углов, то оставшаяся часть развернутого угла между лучами \(OK\) и \(OT\) равна разности большого угла и вычитаемого угла: \( \angle KOT=\angle KOM-\angle TOM=180^\circ-115^\circ=65^\circ\). Здесь использовано свойство смежных углов: сумма смежных углов равна \(180^\circ\), а потому неизвестный смежный угол всегда находится как разность \(180^\circ\) и известного.

б) Ситуация аналогична, но развернутый угол здесь заменен прямым: \( \angle KOM=90^\circ\). Луч \(OT\) внутри этого прямого угла образует угол \( \angle TOM=35^\circ\). Поскольку \( \angle KOT\) и \( \angle TOM\) являются смежными в пределах прямого угла, их сумма равна \( \angle KOM\). Следовательно, величина искомого угла находится вычитанием: \( \angle KOT=\angle KOM-\angle TOM=90^\circ-35^\circ=55^\circ\). Тем самым мы применили то же правило разности, только для суммы, равной \(90^\circ\).

в) Дано, что \( \angle MOP=180^\circ\) — развернутый угол. Внутри него расположены два неперекрывающихся угла с общим вершиной \(O\): \( \angle KOM=45^\circ\) и \( \angle TOP=30^\circ\). Угол \( \angle KOT\) является оставшейся частью развернутого угла после исключения этих двух долей. Поэтому используем аддитивность меры угла: сумма неперекрывающихся углов равна мере большего, а оставшаяся часть получается вычитанием суммы внутренних углов из \(180^\circ\): \( \angle KOT=\angle MOP-(\angle KOM+\angle TOP)=180^\circ-(45^\circ+30^\circ)=105^\circ\). Здесь важно отметить, что углы \( \angle KOM\) и \( \angle TOP\) не накладываются, иначе простое сложение было бы некорректным.

г) Известно: \( \angle MOP=180^\circ\), \( \angle TOM=130^\circ\), \( \angle KOP=140^\circ\). Сначала находим третий смежный к \( \angle TOM\) внутри развернутого угла \(MOP\): \( \angle TOP=\angle MOP-\angle TOM=180^\circ-130^\circ=50^\circ\). Аналогично находим угол, смежный к \( \angle KOP\) в том же развернутом угле: \( \angle KOM=\angle MOP-\angle KOP=180^\circ-140^\circ=40^\circ\). Теперь угол \( \angle KOT\) есть «остаток» развернутого \( \angle MOP\) после вычитания двух внутренних углов \( \angle KOM\) и \( \angle TOP\). По свойству аддитивности меры углов получаем: \( \angle KOT=\angle MOP-(\angle KOM+\angle TOP)=180^\circ-(40^\circ+50^\circ)=90^\circ\). Значит, \( \angle KOT\) является прямым углом.