
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 1.103 Виленкин, Жохов — Подробные Ответы
Вычислите:
а) \(2 — 0,6 : 0,3 + 0,23\);
б) \(7,5 : 10 : 50 : 5 — 0,4\);
в) \(0,82 — 0,4 : 0,6 — 2,5\);
г) \(0,25 : 2 + 3,7 : 10\);
д) \(1,17 — 0,93 : 0,6 + 0,6 — 1,8\).
а) Считаем по порядку: \(2-0{,}6=1{,}4\), затем \(1{,}4\cdot0{,}3=0{,}42\), потом \(0{,}42:6=0{,}07\), и \(0{,}07+0{,}23=0{,}3\). Ответ: \(0{,}3\).
б) Умножаем и делим последовательно: \(7{,}5\cdot10=75\), \(75:50=1{,}5\), \(1{,}5:5=0{,}3\), \(0{,}3\cdot0{,}4=0{,}12\). Ответ: \(0{,}12\).
в) По шагам: \(0{,}82-0{,}4=0{,}42\), \(0{,}42:0{,}6=0{,}7\), \(0{,}7\cdot5=3{,}5\), \(3{,}5-2{,}5=1\). Ответ: \(1\).
г) Последовательно: \(0{,}25\cdot2=0{,}5\), \(0{,}5\cdot0{,}6=0{,}3\), \(0{,}3+3{,}7=4\), \(4:10=0{,}4\). Ответ: \(0{,}4\).
д) Сначала разность столбиком: \(1{,}17-0{,}93=0{,}24\), далее \(0{,}24:0{,}6=0{,}4\), затем \(0{,}4+0{,}6=1\), и \(1\cdot1{,}8=1{,}8\). Ответ: \(1{,}8\).
а) Выполним преобразования по порядку, поясняя каждый шаг. Сначала вычитаем десятичные дроби, выравнивая запятые: \(2-0{,}6=1{,}4\), так как от двух отнимаем шесть десятых, остаётся одна целая и четыре десятых. Затем умножаем полученный результат на десятичную дробь: \(1{,}4\cdot0{,}3=14\cdot3\cdot10^{-2}=42\cdot10^{-2}=0{,}42\); здесь использовано правило умножения десятичных дробей: перемножаем числа без запятых и в ответе отделяем суммарное число знаков после запятой. Далее делим на натуральное число: \(0{,}42:6=42:6\cdot10^{-2}=7\cdot10^{-2}=0{,}07\); деление выполнено поразрядно, можно проверить умножением \(0{,}07\cdot6=0{,}42\). Наконец, складываем десятичные дроби, выравнивая запятые: \(0{,}07+0{,}23=0{,}30=0{,}3\). Ответ: \(0{,}3\).
б) Сначала умножаем на степень десяти, что эквивалентно сдвигу запятой вправо на один разряд: \(7{,}5\cdot10=75\). Затем последовательно делим: \(75:50=\frac{75}{50}=\frac{3}{2}=1{,}5\); здесь обе части дроби сократили на \(25\). Далее \(1{,}5:5=\frac{1{,}5}{5}=\frac{15}{50}=\frac{3}{10}=0{,}3\); удобнее умножить числитель и знаменатель на \(10\), чтобы убрать запятую. Заканчиваем умножением десятичных дробей: \(0{,}3\cdot0{,}4=3\cdot4\cdot10^{-2}=12\cdot10^{-2}=0{,}12\). Ответ: \(0{,}12\).
в) Сначала аккуратно вычитаем: \(0{,}82-0{,}4=0{,}42\), так как \(82\) сотых минус \(40\) сотых дают \(42\) сотых. Затем делим десятичную дробь на десятичную: \(0{,}42:0{,}6=\frac{42}{100}:\frac{6}{10}=\frac{42}{100}\cdot\frac{10}{6}=\frac{420}{600}=\frac{7}{10}=0{,}7\); применили правило деления дробей через умножение на обратную и последующее сокращение на \(60\). Далее умножаем на целое число: \(0{,}7\cdot5=3{,}5\), поскольку \(7\cdot5=35\) и один знак после запятой сохраняется. Наконец, вычитаем десятичные дроби: \(3{,}5-2{,}5=1\); разность одинаковых десятых даёт целое число. Ответ: \(1\).
г) Начинаем с умножения четверти на два: \(0{,}25\cdot2=0{,}5\), что очевидно как половина от единицы. Затем \(0{,}5\cdot0{,}6=5\cdot6\cdot10^{-2}=30\cdot10^{-2}=0{,}3\); перемножили без запятой и вернули два знака после запятой. Складываем с целой и десятичной: \(0{,}3+3{,}7=4{,}0=4\); сумма десятых даёт ещё \(0{,}0\), итого ровно четыре. И делим на десять, что означает сдвиг запятой влево на один разряд: \(4:10=0{,}4\). Ответ: \(0{,}4\).
д) Вычитаем столбиком, выравнивая сотые: \(1{,}17-0{,}93=0{,}24\), так как \(17\) сотых минус \(93\) сотых выполняется с занятием из целой части: \(117\) сотых минус \(93\) сотых равно \(24\) сотых. Далее делим десятичные дроби через приведение к обыкновенным: \(0{,}24:0{,}6=\frac{24}{100}:\frac{6}{10}=\frac{24}{100}\cdot\frac{10}{6}=\frac{240}{600}=\frac{2}{5}=0{,}4\); сократили на \(120\). Потом складываем до целого: \(0{,}4+0{,}6=1\), поскольку сумма дополняющих десятых равна единице. И завершаем умножением на десятичную дробь: \(1\cdot1{,}8=1{,}8\), так как умножение на единицу не изменяет число. Ответ: \(1{,}8\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


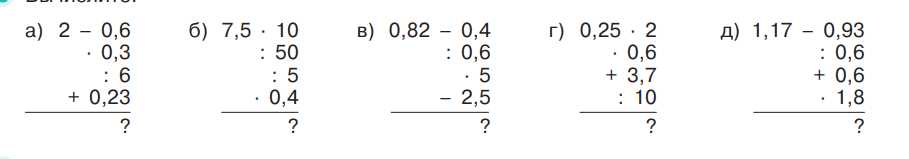



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!