ГДЗ по Математике 5 Класс Часть 2 Задания для самопроверки Страница 189 Мнемозина Виленкин, Жохов — Подробные Ответы

1. Укажите наименьшее трёхзначное натуральное число, которое при делении на 15 даёт остаток 7.

2. Сколько градусов содержит угол, если он составляет \(\frac{2}{3}\) развёрнутого угла?

3. Для приготовления молочного коктейля берут 2 части фруктового сиропа, 3 части сливок и 6 частей мороженого. Сколько граммов сливок потребуется для приготовления 264 г коктейля?

4. Расположите числа 0,035, 0,009, 0,1, 0,0089 в порядке возрастания.

5. Укажите уравнения, для которых число 0,5 является корнем.
а) \(5 : x — 9 = 1\);
в) \(16x — 7x = 4,5\);
б) \((x — 0,3) \cdot 0,1 = 4,7\);
г) \(x + x — \frac{1}{2} = \frac{1}{2}\).

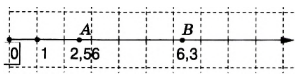
6. Найдите расстояние между точками \(A\) и \(B\) в единичных отрезках.
\(A = 2{,}56\), \(B = 6{,}3\)

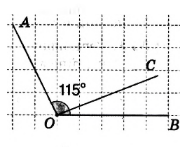
7. Луч \(OC\) делит угол \(AOB\) на два угла, так что \(AOC\) в 4 раза больше \(BOC\).
Укажите величину угла \(AOC\), если \(\angle AOB = 115^\circ\).

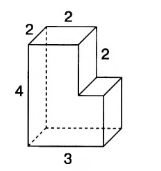
8. Найдите объём фигуры, изображённой на рисунке.
Размеры фигуры: 4, 3, 2, 2, 2

9. Велосипедист первый участок пути проехал за 2 ч со скоростью 14,4 км/ч, а второй участок — за 3 ч со скоростью 12,4 км/ч. Найдите среднюю скорость велосипедиста на всём пути.

10. \(A\) — множество натуральных чисел до 25, которые делятся без остатка на 3.
\(B\) — множество натуральных чисел до 25, которые делятся без остатка на 2.
Укажите пересечение множеств \(A\) и \(B\).

а) \(\{2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24\}\)
б) \(\{6, 12, 18, 24\}\)
в) \(\{2, 3, 6, 12, 18\}\)
г) \(\{1, 2, 3, 6\}\)

1. Наименьшее трёхзначное число, при делении на 15 дающее остаток 7, найдём так:

\(15 \cdot 6 = 90; \quad 90 + 7 = 97\) — не подходит,
\(15 \cdot 7 = 105; \quad 105 + 7 = 112\) — подходит.

Ответ: 112.

2. Развёрнутый угол равен 180°. Найдём \(\frac{2}{3}\) от развёрнутого угла:

\(180 : 3 \cdot 2 = 60 \cdot 2 = 120^\circ\).

Ответ: 120°.

3. Весь коктейль состоит из \(2 + 3 + 6 = 11\) частей.
На одну часть приходится \(264 : 11 = 24\) г.
Сливок потребуется \(3 \cdot 24 = 72\) г.

Ответ: 72 г.

4. Расположим числа по возрастанию:

\(0,0089 < 0,009 < 0,035 < 0,1\).

5. а) \(5 : x — 9 = 1\)
\(5 : x = 1 + 9\)
\(5 : x = 10\)
\(x = 5 : 10\)
\(x = 0,5\) — корень.

в) \(16x — 7x = 4,5\)
\(9x = 4,5\)
\(x = 4,5 : 9\)
\(x = 0,5\) — корень.

б) \((x — 0,3) \cdot 0,1 = 4,7\)
\(x — 0,3 = 4,7 : 0,1\)
\(x — 0,3 = 47\)
\(x = 47 + 0,3\)
\(x = 47,3\) — не корень.

г) \(x + x — \frac{1}{2} = \frac{1}{2}\)
\(2x — \frac{1}{2} = \frac{1}{2}\)
\(2x = \frac{1}{2} + \frac{1}{2}\)
\(2x = 1\)
\(x = 1 : 2\)
\(x = 0,5\) — корень.

Ответ: для уравнений а), в), г) число \(0,5\) является корнем.

6. Расстояние между точками \(A\) и \(B\) равно
\(6,3 — 2,56 = 3,74\) (ед. отр.).

Ответ: \(3,74\) ед. отр.

7. Пусть \(\angle BOC = x^\circ\), тогда \(\angle AOC = 4x^\circ\).
Составим уравнение:
\(x + 4x = 115\)
\(5x = 115\)
\(x = 115 : 5\)
\(x = 23^\circ = \angle BOC\)
\(4x = 4 \cdot 23 = 92^\circ = \angle AOC\).

Ответ: \(\angle AOC = 92^\circ\).

8. Объем прямоугольного параллелепипеда с измерениями 3, 4 и 2 равен \(3 \cdot 4 \cdot 2 = 24\).
Вычитаем объем «отрезанной» части с измерениями 2, 2 и \(3 — 2 = 1\): \(2 \cdot 2 \cdot 1 = 4\).
Объем фигуры равен \(24 — 4 = 20\) куб. ед.

9. За 5 ч велосипедист проехал путь: \(14{,}4 \cdot 2 + 12{,}4 \cdot 3 = 28{,}8 + 37{,}2 = 66\) км.
Средняя скорость: \(\frac{66}{5} = 13{,}2\) км/ч.

10. \(A = \{3, 6, 9, 12, 15, 18, 21, 24\}\) — числа, делящиеся на 3 до 25.
\(B = \{2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24\}\) — числа, делящиеся на 2 до 25.
Пересечение \(A \cap B = \{6, 12, 18, 24\}\).

Ответ: б).

1. Чтобы найти наименьшее трёхзначное число, которое при делении на 15 даёт остаток 7, нужно понять, как устроено деление с остатком. Пусть искомое число — \(n\). Тогда при делении на 15 оно даёт частное \(k\) и остаток 7, то есть можно записать уравнение: \(n = 15 \cdot k + 7\), где \(k\) — целое число. Нужно найти минимальное трёхзначное \(n\), то есть \(100 \leq n \leq 999\).

Для этого подставим разные значения \(k\), начиная с тех, которые дают число около 100. Проверим \(k=6\): \(15 \cdot 6 = 90\), прибавим остаток 7, получаем \(90 + 7 = 97\), что меньше 100, значит, число двузначное и не подходит. Следующее \(k=7\): \(15 \cdot 7 = 105\), прибавим 7, получаем \(105 + 7 = 112\), это уже трёхзначное число. Значит, \(112\) — наименьшее трёхзначное число с остатком 7 при делении на 15.

Таким образом, решение сводится к подбору подходящего частного \(k\), чтобы сумма \(15 \cdot k + 7\) была минимальным трёхзначным числом. Проверка показала, что это число — 112.

2. Развёрнутый угол равен 180°. Нужно найти, сколько градусов составляет \(\frac{2}{3}\) от этого угла. Развёрнутый угол — это угол в прямой линии, равный 180°. Чтобы найти часть угла, нужно умножить 180° на эту часть.

Для вычисления \(\frac{2}{3}\) от 180° сначала делим 180 на 3, получаем 60°, затем умножаем на 2: \(60 \cdot 2 = 120^\circ\). Это и есть искомый угол. Деление и умножение выполняются по правилам работы с дробями и числами, что позволяет найти часть величины.

Таким образом, угол, равный \(\frac{2}{3}\) развёрнутого угла, составляет 120°.

3. Для приготовления молочного коктейля берут 2 части фруктового сиропа, 3 части сливок и 6 частей мороженого. Сначала нужно определить общее количество частей коктейля, сложив все части: \(2 + 3 + 6 = 11\). Это значит, что весь коктейль состоит из 11 равных частей.

Общий вес коктейля 264 г. Чтобы узнать вес одной части, нужно разделить общий вес на количество частей: \(264 : 11 = 24\) г на часть. Теперь, чтобы узнать, сколько граммов сливок потребуется, умножаем количество частей сливок на вес одной части: \(3 \cdot 24 = 72\) г.

Таким образом, для приготовления коктейля потребуется 72 г сливок.

4. Расположение чисел в порядке возрастания требует сравнения их значений с учётом десятичных знаков. Для начала нужно обратить внимание на цифры после запятой и их количество. Число \(0,0089\) меньше числа \(0,009\), потому что при сравнении по разрядам после запятой первая цифра у обоих равна нулю, вторая тоже, третья в первом числе 8, а во втором 9, и так как 8 меньше 9, то \(0,0089 < 0,009\).

Далее сравним \(0,009\) и \(0,035\). Поскольку \(0,009\) — это девять тысячных, а \(0,035\) — тридцать пять тысячных, то очевидно, что \(0,009 < 0,035\). Здесь важно понимать, что при сравнении десятичных дробей, если количество знаков после запятой разное, можно дополнить число нулями справа без изменения его значения, чтобы сравнение было удобнее: \(0,009 = 0,0090\), \(0,035 = 0,0350\).

Наконец, сравним \(0,035\) и \(0,1\). Число \(0,1\) — это одна десятая, а \(0,035\) — тридцать пять тысячных. Поскольку одна десятая больше тридцати пяти тысячных, имеем \(0,035 < 0,1\). Таким образом, все числа упорядочены по возрастанию как \(0,0089 < 0,009 < 0,035 < 0,1\). Это последовательное сравнение цифр в каждом разряде и использование дополнения нулями для удобства сравнения помогает правильно упорядочить десятичные дроби.

5. а) В уравнении \(5 : x — 9 = 1\) сначала нужно изолировать дробь \(5 : x\). Для этого прибавим 9 к обеим частям уравнения, получим \(5 : x = 1 + 9\). Сложив правую часть, имеем \(5 : x = 10\). Теперь задача сводится к нахождению \(x\), при котором деление 5 на \(x\) равно 10. Чтобы найти \(x\), нужно выразить его из равенства \(5 : x = 10\), что эквивалентно \(x = \frac{5}{10}\). После вычисления получаем \(x = 0,5\).

Проверим, подходит ли найденное значение. Подставим \(x = 0,5\) в исходное уравнение: \(5 : 0,5 — 9 = 10 — 9 = 1\), что совпадает с правой частью уравнения. Значит, \(x = 0,5\) является корнем уравнения.

в) Рассмотрим уравнение \(16x — 7x = 4,5\). Сначала упростим левую часть, объединив подобные члены: \(16x — 7x = 9x\). Уравнение примет вид \(9x = 4,5\). Чтобы найти \(x\), разделим обе части уравнения на 9: \(x = \frac{4,5}{9}\). Деление даёт \(x = 0,5\).

Проверим правильность решения, подставив \(x = 0,5\) обратно в уравнение: \(16 \cdot 0,5 — 7 \cdot 0,5 = 8 — 3,5 = 4,5\). Равенство сохраняется, значит, \(x = 0,5\) — корень уравнения.

б) Уравнение \((x — 0,3) \cdot 0,1 = 4,7\) содержит произведение на десятичное число. Чтобы избавиться от множителя \(0,1\), разделим обе части уравнения на \(0,1\), получим \(x — 0,3 = \frac{4,7}{0,1}\). Деление даёт \(x — 0,3 = 47\). Далее прибавим \(0,3\) к обеим частям, чтобы найти \(x\): \(x = 47 + 0,3 = 47,3\).

Подставим \(x = 47,3\) в исходное уравнение: \((47,3 — 0,3) \cdot 0,1 = 47 \cdot 0,1 = 4,7\), что совпадает с правой частью. Значит, корень уравнения — \(x = 47,3\). Число \(0,5\) не является решением этого уравнения.

г) В уравнении \(x + x — \frac{1}{2} = \frac{1}{2}\) сначала объединим одинаковые слагаемые слева: \(x + x = 2x\), тогда уравнение примет вид \(2x — \frac{1}{2} = \frac{1}{2}\). Чтобы избавиться от дроби, прибавим \(\frac{1}{2}\) к обеим частям: \(2x = \frac{1}{2} + \frac{1}{2}\). Складывая дроби, получаем \(2x = 1\).

Далее найдём \(x\), разделив обе части уравнения на 2: \(x = \frac{1}{2}\). Подставим проверку: \(2 \cdot \frac{1}{2} — \frac{1}{2} = 1 — \frac{1}{2} = \frac{1}{2}\), что соответствует правой части уравнения. Значит, \(x = 0,5\) — корень.

Ответ: для уравнений а), в), г) число \(0,5\) является корнем.

6. Расстояние между точками \(A\) и \(B\) находится как разность их координат, если точки расположены на числовой оси. Дано \(A = 2,56\) и \(B = 6,3\). Вычислим расстояние: \(6,3 — 2,56 = 3,74\). Это значение показывает, сколько единичных отрезков содержится между точками \(A\) и \(B\).

Вычисление можно представить в виде столбика:

Результат равен \(3,74\) единицам отрезка.

Ответ: расстояние между точками равно \(3,74\) ед. отр.

7. Пусть угол \(\angle BOC = x^\circ\). По условию, угол \(\angle AOC\) в 4 раза больше, значит \(\angle AOC = 4x^\circ\). Известно, что сумма углов \(\angle BOC\) и \(\angle AOC\) равна углу \(\angle AOB\), то есть \(x + 4x = 115^\circ\).

Объединим подобные слагаемые: \(5x = 115^\circ\). Чтобы найти \(x\), разделим обе части уравнения на 5: \(x = \frac{115}{5} = 23^\circ\). Значит, \(\angle BOC = 23^\circ\).

Теперь найдём \(\angle AOC\), умножив \(x\) на 4: \(4 \cdot 23^\circ = 92^\circ\). Таким образом, угол \(\angle AOC\) равен \(92^\circ\).

Ответ: \(\angle AOC = 92^\circ\).

8. Для нахождения объёма фигуры, изображённой на рисунке, мысленно дорисуем её до полного прямоугольного параллелепипеда, размеры которого равны 3, 4 и 2. Это значит, что объём всего параллелепипеда будет равен произведению его трёх измерений: \(3 \times 4 \times 2 = 24\) кубических единиц. Такой подход позволяет упростить расчёт, выделив объём полной фигуры, из которой потом вычтем лишние части.

Далее необходимо вычесть объём «отрезанной» части фигуры, которая была мысленно добавлена, но не входит в исходную фигуру. Размеры этой части равны 2, 2 и разница между длиной 3 и 2, то есть \(3 — 2 = 1\). Следовательно, объём этой части равен \(2 \times 2 \times 1 = 4\) кубических единиц. Вычитая этот объём из объёма полного параллелепипеда, получаем объём исходной фигуры: \(24 — 4 = 20\) кубических единиц.

Таким образом, итоговый объём фигуры равен \(20\) кубическим единицам. Это решение основано на разбиении сложной фигуры на простые геометрические тела и применении формулы объёма прямоугольного параллелепипеда с последующим вычитанием лишней части.

9. Для нахождения средней скорости велосипедиста на всём пути сначала определим общий путь, который он проехал за два участка. Первый участок длиной 2 часа со скоростью 14,4 км/ч даёт расстояние \(14,4 \times 2 = 28,8\) км. Второй участок длиной 3 часа со скоростью 12,4 км/ч даёт расстояние \(12,4 \times 3 = 37,2\) км. Сложив эти расстояния, найдём полный путь: \(28,8 + 37,2 = 66\) км.

Общее время движения велосипедиста равно сумме времени на оба участка: \(2 + 3 = 5\) часов. Средняя скорость на всём пути определяется как отношение общего пройденного расстояния к общему времени: \(\frac{66}{5} = 13,2\) км/ч. Это значение показывает, с какой скоростью велосипедист двигался в среднем, учитывая оба участка пути.

Таким образом, средняя скорость велосипедиста на всём пути равна \(13,2\) километра в час. При этом важно понимать, что средняя скорость не является простой средней арифметической скоростей на каждом участке, а рассчитывается через общее расстояние и общее время.

10. Множество \(A\) состоит из всех натуральных чисел до 25, которые делятся без остатка на 3. Это числа: 3, 6, 9, 12, 15, 18, 21, 24. Множество \(B\) состоит из всех натуральных чисел до 25, делящихся без остатка на 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24. Пересечение множеств \(A\) и \(B\), то есть \(A \cap B\), — это те числа, которые одновременно делятся и на 3, и на 2, то есть на 6.

Чтобы найти пересечение, нужно выделить общие элементы в обоих множествах: 6, 12, 18, 24. Эти числа делятся и на 3, и на 2 без остатка. Таким образом, пересечение множеств \(A\) и \(B\) равно \(\{6, 12, 18, 24\}\).

Ответ на вопрос — вариант б), поскольку именно этот набор чисел соответствует пересечению множеств натуральных чисел, делящихся на 3 и на 2, до 25 включительно.