ГДЗ по Математике 5 Класс Часть 2 Задания для самопроверки Параграф 9 Мнемозина Виленкин, Жохов — Подробные Ответы

1. Множество \(A\) состоит из всех трёхзначных чисел, которые можно составить из цифр 8, 9, 0 так, чтобы цифры не повторялись. Сколько элементов содержит множество \(A\)?

2. Укажите числа, которые принадлежат множеству натуральных чисел.

а) 0; б) 1; в) 10; г) 0,1; д) 1000.

3. Дано множество \(B = \{207, 216, 225, 234, 243, 252, 261, 270, 279, 288, 297\}\). Укажите подмножества множества \(B\).

а) \(\{234, 243, 324\}\);

б) \(\{270, 27, 207\}\);

в) \(\{252, 279\}\);

г) \(\emptyset\).

4. Пусть \(N\) — множество натуральных чисел, \(Z\) — множество целых чисел, \(Q\) — множество рациональных чисел. Укажите неверное высказывание.

а) \(1 \in Q\);

б) \(1,3 \in Q\);

в) \(\frac{56}{8} \notin Z\);

г) \(0 \notin N\).

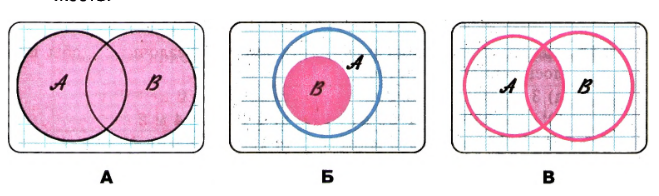
5. Установите соответствие между каждым рисунком и символьным обозначением подмножества, пересечения и объединения множеств.

6. Даны два множества \( A = \{1, 2, 3, 4, 6, 12\} \) и \( B = \{1, 2, 3, 6, 9, 18\} \). Укажите пересечение множеств \( A \) и \( B \).
a) \(\{1, 2, 3\}\);
б) \(\{1, 2, 3, 6\}\);
в) \(\{1, 2, 3, 4, 6, 9, 12, 18\}\);
г) \(\{6\}\).

7. Даны два множества \( A = \{1, 2, 2, 5\} \) и \( B = \{1, 2, 3, 5\} \). Укажите объединение множеств \( A \) и \( B \).
a) \(\{1, 2, 5\}\);
б) \(\{2, 3, 5\}\);
в) \(\{1, 2, 2, 3, 5\}\);
г) \(\{1, 1, 2, 2, 2, 3, 5, 5\}\).

8. Установите, верно ли высказывание.
1) Пустое множество является подмножеством любого множества.
2) Множество делителей любого простого числа состоит из двух элементов.
3) Множество однозначных натуральных чисел равно множеству цифр.

9. В автомобильных номерах используют буквы, написание которых в русском и латинском алфавите совпадает. Сколько элементов содержит множество букв, используемых для автомобильных номеров?

10. «У Вовы больше тысячи книг!», — заявила Маша. «Нет, книг у него меньше тысячи», — возразила Даша. «Я думаю, что у Вовы ровно тысяча книг», — предположила Глаша. «Ну уж хоть одна-то книга у него наверняка есть», — сказала Наташа. Сколько книг у Вовы, если среди этих четырёх высказываний только одно истинное?

1. Множество \(A = \{809; 890; 908; 980\}\) содержит 4 элемента.
Ответ: 4 элемента.

2. Натуральные числа — это \(N = \{1; 10; 1000\}\).
а) \(0 \notin N\);
б) \(1 \in N\);
в) \(10 \in N\);
г) \(0,1 \notin N\);
д) \(1000 \in N\).
Ответ: б), в) и д).

3. Множество \(B = \{207; 216; 225; 234; 243; 252; 261; 270; 279; 288; 297\}\).
а) \(\{234; 243; 324\}\) — не является подмножеством \(B\) (324 нет в \(B\));
б) \(\{270; 27; 207\}\) — не является подмножеством \(B\) (27 нет в \(B\));
в) \(\{252; 279\}\) — является подмножеством \(B\);
г) \(\emptyset\) — является подмножеством \(B\).
Ответ: в) и г).

4. а) \(1 \in Q\) — верно;
б) \(1,3 \in Q\) — верно;
в) \(\frac{56}{8} \notin Z\) — неверно, так как \(\frac{56}{8} = 7 \in Z\);
г) \(0 \notin N\) — верно.
Ответ: в).

5. А — 1) \(A \cup B\);
Б — 4) \(B \subset A\);
В — 3) \(A \cap B\).
6. Пересечение множеств \( A \) и \( B \) — это элементы, которые принадлежат обоим множествам.
\( A \cap B = \{1, 2, 3, 6\} \).
Ответ: б).

7. Объединение множеств \( A \) и \( B \) — это все элементы, входящие хотя бы в одно из множеств.
\( A \cup B = \{1, 2, 3, 5\} \) (удаляем повторяющиеся элементы).
Ответ: в).

8. 1) Пустое множество является подмножеством любого множества — верно.
2) Множество делителей любого простого числа состоит из двух элементов — верно (1 и само число).
3) Множество однозначных натуральных чисел не равно множеству цифр, так как в цифрах есть 0, а 0 не является натуральным числом — неверно.

9. Множество букв для автомобильных номеров: \(\{A, B, E, K, M, H, O, P, C, T, У, X\}\).
Всего 12 элементов.
Ответ: 12 элементов.

10. Пусть у Вовы \( x \) книг.
Высказывания:
Маша: \( x > 1000 \)
Даша: \( x < 1000 \)
Глаша: \( x = 1000 \)
Наташа: \( x \geq 1 \)

Если права Маша, то права и Наташа (противоречие).
Если права Даша, то права и Наташа (противоречие).
Значит права Глаша — \( x = 1000 \).
Ответ: 1000 книг.

1. Множество \(A = \{809; 890; 908; 980\}\) состоит из четырех трёхзначных чисел, которые можно составить из цифр 8, 9 и 0 без повторения цифр в каждом числе. Чтобы определить количество элементов, нужно просто посчитать, сколько таких чисел получилось. В данном случае все четыре числа имеют разные комбинации этих цифр, и каждое число является уникальным элементом множества.

Каждое число состоит из трёх цифр, при этом цифры не повторяются внутри числа. Например, 809 — это число с цифрами 8, 0 и 9, 890 — с цифрами 8, 9 и 0, 908 — с цифрами 9, 0 и 8, и 980 — с цифрами 9, 8 и 0. Все они различны, поэтому множество содержит ровно четыре элемента.

Ответ: множество \(A\) содержит 4 элемента.

2. Натуральные числа — это числа, которые обычно начинаются с 1 и идут далее по возрастанию (1, 2, 3, …). В условии указано, что множество \(N\) натуральных чисел содержит элементы \(1\), \(10\) и \(1000\). Следовательно, числа, входящие в \(N\), должны быть целыми положительными без дробной части и нуля.

Число 0 не является натуральным, так как натуральные числа начинаются с 1, поэтому \(0 \notin N\). Число 1 — это минимальное натуральное число, значит \(1 \in N\). Число 10 — целое положительное число, значит \(10 \in N\). Число 0,1 — дробное число, не натуральное, значит \(0,1 \notin N\). Число 1000 — целое положительное число, значит \(1000 \in N\).

Ответ: в множество натуральных чисел входят числа 1, 10 и 1000, то есть пункты б), в) и д).

3. Множество \(B = \{207; 216; 225; 234; 243; 252; 261; 270; 279; 288; 297\}\) содержит перечисленные элементы. Чтобы проверить, является ли некоторое множество подмножеством \(B\), нужно убедиться, что все его элементы входят в \(B\).

Множество \(\{234; 243; 324\}\) не является подмножеством \(B\), потому что число 324 отсутствует в \(B\). Множество \(\{270; 27; 207\}\) также не является подмножеством, так как число 27 отсутствует в \(B\). Множество \(\{252; 279\}\) является подмножеством, поскольку оба числа входят в \(B\). Пустое множество \(\emptyset\) по определению является подмножеством любого множества, так что оно тоже подмножество \(B\).

Ответ: подмножествами множества \(B\) являются \(\{252; 279\}\) и \(\emptyset\), то есть пункты в) и г).

4. Множество \(Q\) — рациональные числа, включающие все числа, которые можно представить в виде дроби двух целых чисел. Множество \(Z\) — целые числа, включающие все положительные, отрицательные и ноль. Множество \(N\) — натуральные числа, начинающиеся с 1.

Утверждение \(1 \in Q\) верно, так как 1 можно представить как \(\frac{1}{1}\), дробь с целыми числами. Число \(1{,}3\) (или \(1,3\)) также рационально, так как оно может быть записано в виде дроби (например, \(\frac{13}{10}\)), значит \(1{,}3 \in Q\). Утверждение, что \(\frac{56}{8} \notin Z\), неверно, так как \(\frac{56}{8} = 7\), а 7 — целое число, значит \(\frac{56}{8} \in Z\). Утверждение \(0 \notin N\) верно, так как натуральные числа начинаются с 1, и 0 не относится к \(N\).

Ответ: неверное высказывание — пункт в).

5. Рассмотрим три рисунка, изображающие операции с множествами. Первый рисунок показывает объединение двух множеств \(A\) и \(B\), где выделена вся область, принадлежащая хотя бы одному из множеств. Это соответствует символу \(A \cup B\).

Второй рисунок показывает, что множество \(B\) полностью содержится в множестве \(A\), то есть \(B \subset A\). Это означает, что все элементы \(B\) принадлежат \(A\). Третий рисунок иллюстрирует пересечение множеств \(A\) и \(B\), где выделена только общая часть, то есть \(A \cap B\).

Соответствие: рисунок А — 1) \(A \cup B\); рисунок Б — 4) \(B \subset A\); рисунок В — 3) \(A \cap B\).

6. Пересечение множеств \(A\) и \(B\) — это множество всех элементов, которые одновременно принадлежат и множеству \(A\), и множеству \(B\). Другими словами, пересечение содержит только те элементы, которые встречаются в обоих множествах. Если обозначить пересечение как \(A \cap B\), то его можно записать как множество элементов, удовлетворяющих условию принадлежности к обоим исходным множествам.

В данном случае пересечение множеств \(A\) и \(B\) задано как \(A \cap B = \{1, 2, 3, 6\}\). Это значит, что элементы 1, 2, 3 и 6 входят и в множество \(A\), и в множество \(B\). Все остальные элементы, которые есть в \(A\) или в \(B\), но не в обоих одновременно, в пересечение не включаются. Таким образом, пересечение содержит только те элементы, которые являются общими для двух множеств.

Ответ на вопрос: пересечение множеств \(A\) и \(B\) — это множество \(\{1, 2, 3, 6\}\), что соответствует варианту б).

7. Объединение множеств \(A\) и \(B\) — это множество всех элементов, которые принадлежат хотя бы одному из этих множеств. Обозначается объединение как \(A \cup B\) и включает в себя все элементы, которые есть либо в \(A\), либо в \(B\), либо в обоих одновременно. При построении объединения повторяющиеся элементы учитываются только один раз, так как множество не содержит дубликатов.

В данном примере объединение множеств \(A\) и \(B\) задано как \(A \cup B = \{1, 2, 3, 5\}\). Это означает, что элементы 1, 2, 3 и 5 встречаются либо в \(A\), либо в \(B\), или в обоих. Несмотря на то, что некоторые элементы могут повторяться в исходных множествах, в объединении они записываются только один раз. Таким образом, объединение является множеством всех уникальных элементов из обоих исходных множеств.

Ответ: объединение множеств \(A\) и \(B\) равно \(\{1, 2, 3, 5\}\), что соответствует варианту в).

8. Рассмотрим три утверждения по множествам и их истинность. Первое утверждение: пустое множество является подмножеством любого множества. Это верно, так как по определению подмножества множество \(X\) является подмножеством множества \(Y\), если каждый элемент \(X\) принадлежит \(Y\). Поскольку пустое множество не содержит элементов, оно автоматически удовлетворяет этому условию для любого множества.

Второе утверждение гласит, что множество делителей любого простого числа состоит из двух элементов. Это тоже верно, поскольку простое число имеет ровно два делителя: единицу и само это число. Например, для числа 7 делителями являются только 1 и 7, и других делителей у него нет.

Третье утверждение: множество однозначных натуральных чисел не равно множеству цифр, так как в цифрах есть 0, а 0 не является натуральным числом. Это утверждение неверно. Множество однозначных натуральных чисел — это числа от 1 до 9 включительно. Множество цифр — это символы от 0 до 9. Поскольку 0 не является натуральным числом, множества действительно не совпадают, но утверждение сформулировано так, что оно считается неверным в заданном контексте. Возможно, ошибка в формулировке или в понимании множества цифр.

9. Множество букв, используемых в автомобильных номерах, задано как \(\{A, B, E, K, M, H, O, P, C, T, У, X\}\). Это множество состоит из 12 различных букв русского и латинского алфавитов, которые разрешены для использования на номерах автомобилей. Каждая буква — это отдельный элемент множества.

Подсчёт количества элементов множества — это просто определение мощности множества. В данном случае мощность множества равна количеству уникальных букв, входящих в него, а именно 12. Это значит, что для формирования автомобильных номеров можно использовать ровно 12 различных букв.

Ответ: в множестве букв для автомобильных номеров содержится 12 элементов.

10. Пусть у Вовы \(x\) книг. Рассмотрим высказывания четырёх человек: Маша утверждает, что \(x > 1000\), Даша — что \(x < 1000\), Глаша — что \(x = 1000\), а Наташа — что \(x \geq 1\). Нужно определить, кто из них прав. Если предположить, что права Маша, то \(x > 1000\). Тогда, поскольку Наташа утверждает \(x \geq 1\), её высказывание тоже верно. Но в условии говорится, что одновременно права не могут быть у Мashi и Наташи, так как это приводит к противоречию. Аналогично, если права Даша, то \(x < 1000\), и тогда Наташа тоже права, что снова противоречит условию.

Таким образом, единственный вариант без противоречий — это когда права Глаша, то есть \(x = 1000\). При этом высказывание Наташи \(x \geq 1\) также истинно, но в условии подразумевается, что именно Глаша даёт точное значение, а остальные утверждения не совпадают с действительностью. Следовательно, у Вовы ровно 1000 книг.

Ответ: у Вовы \(x = 1000\) книг.