ГДЗ по Математике 5 Класс Часть 2 Задания для самопроверки Параграф 8 Мнемозина Виленкин, Жохов — Подробные Ответы

1. Укажите название величины, равной 1 % квадратного метра.

а) квадратный сантиметр;

б) сотка (ар);

в) квадратный дециметр;

г) гектар.

2. Представьте обыкновенную дробь в виде процентов.

а) \(\frac{1}{2}\);

б) \(\frac{1}{4}\);

в) \(\frac{3}{20}\);

г) \(\frac{2}{5}\).

3. Со склада 25 % картофеля отправили в магазин. Сколько килограммов было отправлено в магазин, если на складе было 64 360 кг?

4. Сколько человек ежедневно перевозит московское метро, если на 1 % всех пассажиров приходится около 70 тыс. человек?

5. Сколько будет стоить куртка, цена которой 6700 р., если она будет продаваться со скидкой 5 %?

6. Чему равна длина пути, если 10 % этого пути составляют 78 км?

7. Дневной план завода составляет 800 деталей. Какой процент плана был сделан в первой половине дня, если было изготовлено 384 детали?

8. Магазин планировал продать 75 холодильников, а продал 90. Сколько процентов от плана составляют проданные холодильники?

9. Сколько процентов соли содержит раствор, приготовленный из 60 г соли и 140 г воды?

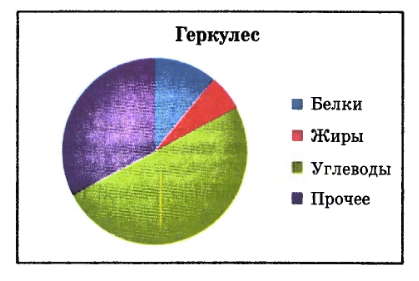
10. На диаграмме показано содержание питательных веществ в геркулесе. Определите по диаграмме, содержание каких веществ составляет 50 %.

1. 1 дм² равен 1 % от 1 м², так как:
\(1 \text{ м}^2 = 100 \text{ дм}^2 \Rightarrow 100 : 100 \cdot 1 = 1 \text{ дм}^2\).

Ответ: в) квадратный дециметр.

2. а) \(\frac{1}{2} = 0{,}5 = 50\%\);
б) \(\frac{1}{4} = 0{,}25 = 25\%\);
в) \(\frac{3}{20} = 0{,}15 = 15\%\);
г) \(\frac{2}{5} = 0{,}4 = 40\%\).

3. Отправлено в магазин: \(64\,360 : 100 \cdot 25 = 643{,}6 \cdot 25 = 16\,090 \text{ кг}\).
Ответ: 16 090 кг.

4. Ежедневно московское метро перевозит: \(70 : 1 \cdot 100 = 70 \cdot 100 = 7\,000 \text{ тыс} = 7 \text{ млн человек}\).
Ответ: 7 млн человек.

5. 1) Скидка: \(6\,700 : 100 \cdot 5 = 67 \cdot 5 = 335 \text{ руб}\).
2) Цена куртки: \(6\,700 — 335 = 6\,365 \text{ руб}\).
Ответ: 6 365 руб.

6. Длина пути равна: \( 78 \div 10 \cdot 100 = 7{,}8 \cdot 100 = 780 \) км.
Ответ: 780 км.

7. Процент плана, сделанного в первой половине дня:
\( 384 \div 800 \cdot 100 = 0{,}48 \cdot 100 = 48 \% \).
Ответ: 48 % плана.

8. Процент проданных холодильников от плана:
\( 90 \div 75 \cdot 100 = 1{,}2 \cdot 100 = 120 \% \).
Ответ: 120 % плана.

9. Масса раствора: \( 60 + 140 = 200 \) г.
Процент соли в растворе:
\( 60 \div 200 \cdot 100 = 0{,}3 \cdot 100 = 30 \% \).
Ответ: 30 % соли.

10. Половину, или 50 %, в геркулесе составляют углеводы.
Ответ: углеводы.

1. 1 дм² равен 1 % от 1 м², потому что площадь в квадратных метрах и квадратных дециметрах связана через коэффициент 100. Это происходит из-за того, что 1 метр равен 10 дециметрам, а площадь — это квадрат длины, поэтому \(1 \text{ м} = 10 \text{ дм}\) означает, что \(1 \text{ м}^2 = 10^2 \text{ дм}^2 = 100 \text{ дм}^2\). Таким образом, один квадратный метр содержит 100 квадратных дециметров.

Чтобы найти, чему равен 1 % от площади в 1 м², нужно разделить 100 дм² на 100, так как 1 % — это одна сотая часть: \(100 : 100 = 1 \text{ дм}^2\). Это значит, что 1 дм² составляет ровно 1 % от 1 м². Именно поэтому правильный ответ — квадратный дециметр.

Таким образом, если рассматривать площадь в квадратных метрах и переводить проценты в площадь, то 1 % от площади 1 м² — это 1 дм². Это важное соотношение помогает при переводе единиц измерения площади и при решении задач с процентами площади.

2. Чтобы представить обыкновенную дробь в виде процентов, нужно сначала преобразовать дробь в десятичное число, а затем умножить на 100, так как процент — это сотая часть числа.

а) Для дроби \(\frac{1}{2}\) делим 1 на 2, получаем \(0{,}5\). Умножаем на 100: \(0{,}5 \cdot 100 = 50\%\). Значит, \(\frac{1}{2}\) равна 50 %.

б) Для дроби \(\frac{1}{4}\) делим 1 на 4, получаем \(0{,}25\). Умножаем на 100: \(0{,}25 \cdot 100 = 25\%\). Значит, \(\frac{1}{4}\) равна 25 %.

в) Для дроби \(\frac{3}{20}\) делим 3 на 20, получаем \(0{,}15\). Умножаем на 100: \(0{,}15 \cdot 100 = 15\%\). Значит, \(\frac{3}{20}\) равна 15 %.

г) Для дроби \(\frac{2}{5}\) делим 2 на 5, получаем \(0{,}4\). Умножаем на 100: \(0{,}4 \cdot 100 = 40\%\). Значит, \(\frac{2}{5}\) равна 40 %.

Этот процесс позволяет быстро и точно перевести любую обыкновенную дробь в процентное выражение через преобразование в десятичное число и умножение на 100.

3. Для определения количества картофеля, отправленного в магазин, нужно найти 25 % от общего количества на складе. Известно, что на складе было 64 360 кг картофеля. Чтобы найти 25 %, сначала делим 64 360 на 100, чтобы найти 1 %: \(64\,360 : 100 = 643{,}6\).

Далее умножаем 1 % на 25, так как нужно 25 %: \(643{,}6 \cdot 25 = 16\,090\). Это количество килограммов картофеля, отправленного в магазин. Такой способ вычисления процентов от числа используется часто и помогает быстро получить нужный результат.

Итог: из 64 360 кг картофеля 16 090 кг были отправлены в магазин, что соответствует 25 % от всей массы.

4. Чтобы найти, сколько человек ежедневно перевозит московское метро, если 1 % всех пассажиров составляет около 70 тыс. человек, нужно умножить количество пассажиров, соответствующих 1 %, на 100. Это связано с тем, что 100 % — это вся масса пассажиров.

Дано: 1 % = 70 тыс. человек. Тогда общее количество пассажиров равно \(70 \cdot 100 = 7\,000\) тыс., что составляет 7 миллионов человек. Такой расчет позволяет перейти от части к целому, используя процентное соотношение.

Таким образом, ежедневно московское метро перевозит около 7 миллионов человек, что показывает масштаб пассажиропотока.

5. Для определения цены куртки со скидкой 5 % сначала вычислим размер скидки от исходной цены 6700 рублей. Для этого нужно найти 5 % от 6700. Сначала делим 6700 на 100, чтобы найти 1 %: \(6\,700 : 100 = 67\).

Затем умножаем 1 % на 5, чтобы получить 5 %: \(67 \cdot 5 = 335\) рублей — это размер скидки. Далее вычитаем эту скидку из исходной цены: \(6\,700 — 335 = 6\,365\) рублей — новая цена куртки.

Такой способ позволяет быстро вычислить цену товара после применения скидки, используя базовые операции с процентами.

6. Длина пути равна: сначала нужно понять, что 10 % пути составляют 78 километров. Чтобы найти весь путь, нужно разделить известную часть на её процентное выражение в десятичном виде. Процент 10 % в десятичной форме равен 0,1. Тогда длина всего пути будет равна \( \frac{78}{0{,}1} \). Деление 78 на 0,1 эквивалентно умножению на 10, поэтому получаем \( 78 \cdot 10 = 780 \) километров. Это значит, что весь путь составляет 780 км.

Таким образом, мы используем формулу для нахождения полного значения по известному проценту: \( \text{Весь путь} = \frac{\text{Часть}}{\text{Доля в десятичной форме}} \). В данном случае часть — это 78 км, а доля — 10 % или 0,1. Полученное число 780 км — это ответ задачи, показывающий, что если 10 % пути — это 78 км, то весь путь равен 780 км.

Это классическая задача на нахождение полного значения по известной части и проценту. Важно помнить, что при работе с процентами нужно переводить их в десятичный вид для удобства вычислений. Здесь 10 % — это 0,1, и деление на 0,1 эквивалентно умножению на 10, что упрощает вычисления.

7. В первой половине дня было сделано 384 детали, а дневной план завода составляет 800 деталей. Чтобы узнать, какой процент плана выполнен, нужно найти отношение сделанных деталей к запланированным и умножить на 100 %. Формула для этого: \( \frac{384}{800} \cdot 100 \). Сначала делим 384 на 800, получая 0,48, затем умножаем на 100, что даёт 48 %. Это означает, что за первую половину дня выполнено 48 % дневного плана.

Такое вычисление показывает, какую часть от общего запланированного объёма работы удалось выполнить за первую половину дня. Мы видим, что 384 детали — это меньше половины от 800, и именно 48 % от всего плана. Это важно для контроля выполнения производства и планирования дальнейшей работы.

В задачах подобного типа всегда нужно помнить, что процент — это отношение части к целому, выраженное в сотых долях. Поэтому сначала нужно вычислить дробь, показывающую долю выполненного плана, а затем умножить её на 100, чтобы получить процент.

8. Магазин планировал продать 75 холодильников, а фактически продал 90. Чтобы узнать, сколько процентов от плана составляют проданные холодильники, нужно разделить фактическое количество на плановое и умножить на 100 %. Формула: \( \frac{90}{75} \cdot 100 \). Делим 90 на 75, получаем 1,2, затем умножаем на 100, что равно 120 %. Это значит, что магазин продал на 20 % больше холодильников, чем планировал.

Такое вычисление помогает понять, насколько превышен или недовыполнен план продаж. Значение 120 % показывает, что продажи превысили план на 20 %, что является положительным результатом для магазина. Этот способ вычисления применяется для оценки выполнения планов в процентах.

Важно понимать, что при значении больше 100 % говорят о перевыполнении плана. В задаче мы видим именно такой случай, и вычисления позволяют количественно оценить этот перевыполненный объём.

9. Для определения процента соли в растворе сначала нужно найти массу всего раствора, сложив массу соли и массу воды. Масса соли — 60 г, масса воды — 140 г, значит масса раствора равна \( 60 + 140 = 200 \) г. Далее, чтобы найти процент соли в растворе, нужно разделить массу соли на массу всего раствора и умножить на 100 %. Формула: \( \frac{60}{200} \cdot 100 \).

Делим 60 на 200, получается 0,3, умножаем на 100, получаем 30 %. Это означает, что раствор содержит 30 % соли по массе. Такой способ вычисления широко используется для определения концентрации веществ в растворах.

Таким образом, процентное содержание вещества в растворе — это отношение массы вещества к массе всего раствора, выраженное в процентах. Это позволяет оценить концентрацию и использовать данные для различных химических и технических расчетов.

10. В геркулесе содержатся три основных вида питательных веществ: белки, жиры и углеводы. По условию задачи и диаграмме видно, что углеводы занимают ровно половину состава, то есть 50 %. Это означает, что если весь состав геркулеса принять за 100 %, то углеводы будут составлять \(50\%\) от этого количества. Такой показатель говорит о том, что углеводы являются доминирующим компонентом в составе продукта.

Для понимания, почему именно углеводы составляют половину, можно рассмотреть, что сумма всех составляющих питательных веществ равна \(100\%\). Если углеводы занимают \(50\%\), то оставшиеся \(50\%\) делятся между белками и жирами. Это можно записать как уравнение: \(50\% + x + y = 100\%\), где \(x\) — процент белков, а \(y\) — процент жиров. Поскольку углеводы занимают именно половину, остальные вещества вместе составляют вторую половину. Это подтверждает, что углеводы — главная часть состава.

Таким образом, исходя из данных диаграммы и условия, можно сделать вывод, что углеводы составляют \(50\%\) геркулеса. Это значит, что если взять, например, 100 грамм геркулеса, то 50 грамм из них будут углеводами. Именно поэтому правильный ответ — углеводы.