ГДЗ по Математике 5 Класс Часть 2 Номер 998 Мнемозина Виленкин, Жохов — Подробные Ответы

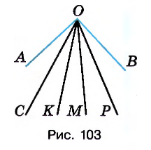
Угол \(AOB\) на рисунке 103 разделён на 5 равных углов. Назовите углы, которые составляют \(\frac{3}{5}\) угла \(AOB\). Найдите величину угла \(COP\), если угол \(AOB\) равен \(100^\circ\).

\( \frac{3}{5} \) угла \( AOB \) составляют углы: \( \angle AOM; \angle COP; \angle KOB \).

\( \angle COP = 100 : 5 \cdot 3 = 20 \cdot 3 = 60^\circ \).

\( \frac{3}{5} \) угла \( AOB \) означает, что весь угол \( AOB \) разбит на части, сумма которых равна \( \frac{3}{5} \) этого угла. В условии указано, что \( \frac{3}{5} \) угла \( AOB \) составляют углы \( \angle AOM \), \( \angle COP \) и \( \angle KOB \). Это значит, что если весь угол \( AOB \) принять за 1 (или 100 %), то сумма этих трёх углов равна именно \( \frac{3}{5} \) от этого целого угла.

Для нахождения величины угла \( \angle COP \) используется пропорция, основанная на том, что весь угол \( AOB \) равен 100°. Тогда \( \frac{3}{5} \) от 100° — это сумма углов \( \angle AOM \), \( \angle COP \) и \( \angle KOB \). Чтобы найти конкретно \( \angle COP \), нужно разделить 100 на 5, так как знаменатель дроби 5, и умножить на 3 — числитель дроби. То есть вычисление идет так: \( 100 : 5 \cdot 3 = 20 \cdot 3 = 60^\circ \). Это означает, что угол \( \angle COP \) равен 60°.

Таким образом, мы использовали дробь \( \frac{3}{5} \) для определения доли угла \( AOB \), которая состоит из трёх углов, и нашли конкретное значение одного из них — \( \angle COP \). Деление 100 на 5 показывает, чему равна одна часть угла \( AOB \), а умножение на 3 — сколько таких частей занимает сумма углов. Итоговый результат — \( \angle COP = 60^\circ \).