
Учебник по математике для 5 класса «Мнемозина» авторов Виленкин и Жохов представляет собой качественное пособие, которое активно используется в школьной программе. Этот учебник сочетает в себе подробные теоретические материалы, интересные задачи и увлекательные примеры, что делает его полезным инструментом для формирования базовых знаний и навыков у школьников.
ГДЗ по Математике 5 Класс Часть 2 Номер 997 Мнемозина Виленкин, Жохов — Подробные Ответы
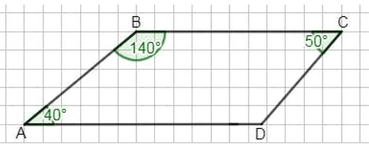
Начертите четырёхугольник \(ABCD\), у которого \(\angle A = 40^\circ\), \(\angle B = 140^\circ\), \(\angle C = 50^\circ\). Измерьте величину угла \(D\).
Угол \(D\) можно найти, зная, что сумма углов параллелограмма равна \(360^\circ\), а противоположные углы равны.
В параллелограмме сумма соседних углов равна \(180^\circ\), значит
\( \angle A + \angle B = 180^\circ \).
Из условия:
\( \angle A = 40^\circ \), \( \angle B = 140^\circ \).
Также
\( \angle C = 50^\circ \).
Угол \(D\) смежен с углом \(C\), значит
\( \angle D + \angle C = 180^\circ \),
откуда
\( \angle D = 180^\circ — 50^\circ = 130^\circ \).
Ответ: \( \angle D = 130^\circ \).
Угол \(D\) в параллелограмме можно определить, используя свойства углов и их взаимосвязь. В параллелограмме противоположные углы равны, а сумма соседних углов равна \(180^\circ\). Из рисунка видно, что угол \(A\) равен \(40^\circ\), а угол \(B\) — \(140^\circ\). Эти два угла являются соседними, поэтому их сумма должна быть равна \(180^\circ\). Это подтверждает, что углы на одной стороне параллелограмма дополняют друг друга до прямой линии, что является характерным свойством параллелограмма.
Далее, угол \(C\) задан как \(50^\circ\). Поскольку \(C\) и \(D\) — также смежные углы, они должны в сумме давать \(180^\circ\). Это связано с тем, что стороны \(CD\) и \(AB\) параллельны, а \(BC\) и \(AD\) — тоже параллельны, поэтому углы при вершинах \(C\) и \(D\), лежащие на одной стороне параллелограмма, являются смежными и их сумма равна \(180^\circ\). Таким образом, чтобы найти угол \(D\), нужно из \(180^\circ\) вычесть угол \(C\).
Выполним вычисление: \( \angle D = 180^\circ — 50^\circ = 130^\circ \). Это значение соответствует углу \(D\), который дополняет угол \(C\) до \(180^\circ\). Итоговое значение угла \(D\) равно \(130^\circ\), что согласуется с геометрическими свойствами параллелограмма и данными на рисунке. Таким образом, используя свойства параллелограмма и знания о смежных углах, мы нашли искомый угол.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!