ГДЗ по Математике 5 Класс Часть 2 Номер 996 Мнемозина Виленкин, Жохов — Подробные Ответы

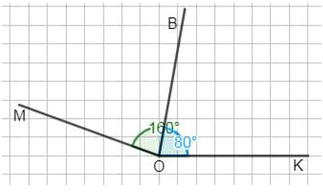
Начертите угол \(MOK\) в \(160^\circ\). Проведите луч \(OB\) так, чтобы он разделил угол \(MOK\) пополам. Как называется такой луч?

Луч \(OV\) называется биссектрисой угла \(MOK\).

Луч \(OV\) делит угол \(MOK\) на два равных угла:

\(\angle MOB = \angle BOK = 80^\circ\).

Луч \(OV\) называется биссектрисой угла \(MOK\), потому что он проходит из вершины угла \(O\) и делит этот угол на две равные части. В геометрии биссектриса угла — это луч, который выходит из вершины угла и делит его на два угла с одинаковой мерой. В данном случае угол \(MOK\) образован лучами \(OM\) и \(OK\), а луч \(OV\) лежит внутри этого угла и делит его на две равные части.

Чтобы понять, почему луч \(OV\) является биссектрисой, нужно обратить внимание на величины углов, которые он образует с лучами \(OM\) и \(OK\). Согласно рисунку, угол \(MOK\) равен сумме углов \(MOB\) и \(BOK\). Из условия видно, что угол \(MOB\) равен \(80^\circ\), и угол \(BOK\) также равен \(80^\circ\). Это означает, что луч \(OV\) делит угол \(MOK\) на два равных угла по \(80^\circ\) каждый. Следовательно, сумма этих углов равна \(160^\circ\), что и есть величина угла \(MOK\).

Таким образом, луч \(OV\) действительно является биссектрисой угла \(MOK\), так как он делит этот угол на два равных угла, то есть выполняет основное свойство биссектрисы. Величина каждого из углов \(MOB\) и \(BOK\) равна \(80^\circ\), что подтверждает правильность определения биссектрисы. Это важное свойство используется в различных задачах геометрии для нахождения углов, построения и доказательств.