ГДЗ по Математике 5 Класс Часть 2 Номер 995 Мнемозина Виленкин, Жохов — Подробные Ответы

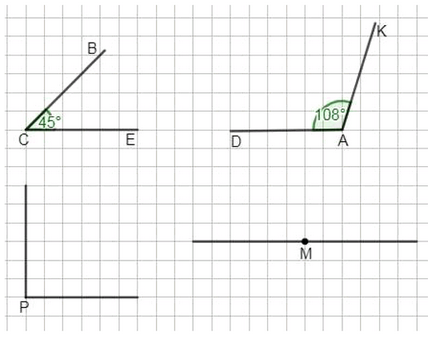
Начертите острый угол \(BCE\) и тупой угол \(DAK\) и определите их градусные меры. Начертите прямой угол \(P\) и развёрнутый угол \(M\). Какова градусная мера прямого угла? развёрнутого угла? Какую часть развёрнутого угла составляет угол в \(1^\circ\)?

∠BCE = 45° — острый угол;
∠DAK = 108° — тупой угол;
∠P = 90° — прямой угол;
∠M = 180° — развернутый угол.

Угол в 1° составляет \( \frac{1}{180} \) часть развернутого угла.

∠BCE = 45° — острый угол. Это означает, что угол между лучами BC и CE меньше 90°. Острый угол всегда находится в интервале от 0° до 90°, поэтому значение 45° подходит под это определение. Такой угол часто встречается в геометрии и характеризуется тем, что его вершина образует «острый» поворот между двумя лучами.

Угол измеряется в градусах, где полный круг равен 360°. Значение 45° — это ровно четверть прямого угла, так как прямой угол равен 90°. Таким образом, угол BCE можно считать равным половине прямого угла, что визуально можно увидеть на рисунке, где угол явно меньше угла прямого.

∠DAK = 108° — тупой угол. Тупой угол — это угол, который больше 90°, но меньше 180°. Значение 108° попадает в этот диапазон, поэтому угол DAK является тупым. Он показывает, что лучи DA и AK расходятся под углом, который шире, чем прямой, но не достигает развернутого угла.

Тупой угол часто встречается в различных геометрических фигурах, например, в трапециях или многоугольниках с углами больше 90°. В данном случае угол 108° больше прямого на 18°, что указывает на более «открытый» поворот между лучами, чем у острого угла.

∠P = 90° — прямой угол. Прямой угол — это угол ровно в 90°, который образует перпендикулярное пересечение двух лучей или отрезков. На рисунке угол P изображён с точной отметкой 90°, что подтверждает его статус прямого угла.

Прямой угол является базовым понятием в геометрии, так как он служит основой для определения многих других углов и фигур. Он соответствует четверти полного круга и часто используется как эталон для измерения других углов.

∠M = 180° — развернутый угол. Развернутый угол равен 180°, что означает, что лучи, образующие этот угол, лежат на одной прямой линии, но направлены в противоположные стороны. В этом случае угол M — это линия, проходящая через точку M, где обе части образуют прямую.

Развернутый угол часто используется для обозначения углов, которые не имеют «изгиба», то есть находятся в одной плоскости и образуют прямую линию. Это важное понятие для понимания линейных углов и их свойств.

Угол в 1° составляет \(\frac{1}{180}\) часть развернутого угла, так как весь развернутый угол равен 180°. Это означает, что каждый градус — это маленькая часть полного развернутого угла, и если разделить развернутый угол на 180 равных частей, каждая часть будет равна одному градусу.

Такое деление угла на градусы позволяет точно измерять и сравнивать углы различной величины. Градус как единица измерения углов является стандартом в геометрии и тригонометрии, обеспечивая удобство и точность в расчетах.