ГДЗ по Математике 5 Класс Часть 2 Номер 991 Мнемозина Виленкин, Жохов — Подробные Ответы

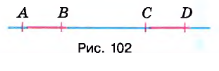
На прямой отмечены точки \( A, B, C \) и \( D \) (рис. 102) так, что \( AB = CD \). Поставьте вместо звёздочки знак \( <, > \) или \( = \) так, чтобы для длин отрезков получилось верное равенство или неравенство:

а) \( BA * DC \);

б) \( AC * BD \);

в) \( AC * CB \);

г) \( AD * BC \).

Известно, что \(AB = CD\).

а) \(BA = DC\) — верно, так как отрезки равны и направления не меняют длину.

б) \(AC > CB\), так как \(AC = AB + BC\), а \(AB > 0\), значит \(AC > BC\).

в) \(AC = BD\), так как \(AC = AB + BC\), \(BD = BC + CD\), при \(AB = CD\) получаем \(AC = BD\).

г) \(AD > BC\), так как \(AD = AB + BD\), а \(BD > 0\), следовательно \(AD > BC\).

а) Известно, что \(AB = CD\). Поскольку длины отрезков равны, то и отрезки \(BA\) и \(DC\) будут равны, так как они представляют те же отрезки, но направленные в обратную сторону. Направление отрезка не влияет на его длину, поэтому \(BA = AB = CD = DC\). Таким образом, равенство \(BA = DC\) справедливо по свойству равенства длин отрезков.

Это равенство подтверждается тем, что при смене порядка точек в обозначении отрезка длина не меняется. Например, отрезок \(AB\) и отрезок \(BA\) — это один и тот же отрезок, просто ориентированный в противоположную сторону, поэтому их длины совпадают. Аналогично для \(CD\) и \(DC\).

б) Рассмотрим неравенство \(AC > CB\). По условию, \(AC = AB + BC\). Поскольку длины отрезков \(AB\) и \(BC\) положительны, сумма \(AB + BC\) будет больше, чем длина одного из слагаемых, в частности \(BC\). Следовательно, \(AC > BC\), что и доказывает неравенство \(AC > CB\).

Здесь важно понимать, что точка \(C\) лежит на отрезке \(AB\) или на продолжении отрезка, и сумма двух отрезков \(AB\) и \(BC\) равна длине отрезка \(AC\). Поэтому длина \(AC\) обязательно больше длины \(BC\), так как к \(BC\) добавляется дополнительный положительный отрезок \(AB\).

в) Рассмотрим равенство \(AC = BD\). Из условия известно, что \(AC = AB + BC\), а также \(BD = BC + CD\). При этом дано, что \(AB = CD\). Подставляя это в равенство для \(BD\), получаем \(BD = BC + AB\).

Сравнивая \(AC = AB + BC\) и \(BD = BC + AB\), видим, что они совпадают, так как сложение чисел коммутативно. Значит, \(AC = BD\). Это равенство основано на равенстве соответствующих отрезков и свойстве сложения чисел.

г) Рассмотрим неравенство \(AD > BC\). Отрезок \(AD\) можно представить как сумму двух отрезков: \(AD = AB + BD\). Из предыдущего пункта известно, что \(BD = BC + CD\), а также дано \(AB = CD\).

Подставляя, получаем \(AD = AB + BD = AB + BC + CD\). Поскольку \(AB = CD\), тогда \(AD = BC + 2AB\). Так как \(AB > 0\), это означает, что \(AD > BC\). Таким образом, длина отрезка \(AD\) всегда больше длины отрезка \(BC\).