ГДЗ по Математике 5 Класс Часть 2 Номер 988 Мнемозина Виленкин, Жохов — Подробные Ответы

Выполните рисунки:
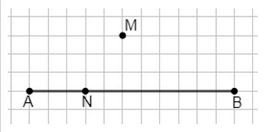
а) начертите отрезок и отметьте точку, лежащую на отрезке, и точку, не лежащую на нём;
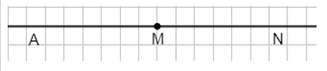
б) начертите прямую и отметьте на ней точку \( M \); ответьте, как называются части, на которые точка \( M \) делит прямую;
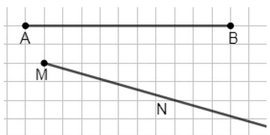
в) начертите отрезок и луч так, чтобы они не пересекались; чтобы отрезок лежал на луче; чтобы отрезок и луч имели одну общую точку;
г) начертите угол и прямую так, чтобы прямая пересекала только одну сторону угла.

а) Точка \( N \) лежит на отрезке \( AB \); точка \( M \) не лежит на отрезке \( AB \).

б) Точка \( M \) делит прямую \( AN \) на два луча: \( MA \) и \( MN \).

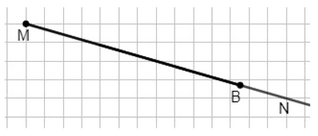
в) Отрезок и луч не пересекаются: \( M \in AB, N \notin AB \).

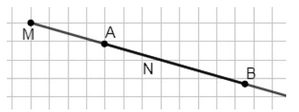
Отрезок лежит на луче: \( M \in NB, A \in NB \).

Отрезок и луч имеют общую точку: \( B \in MN \).

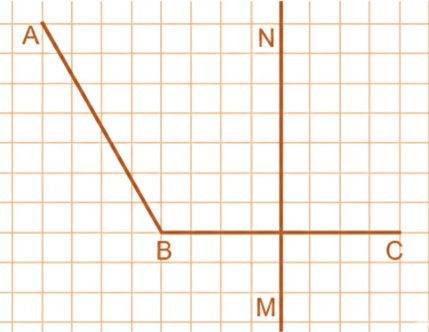
г) Прямая пересекает одну сторону угла: прямая проходит через точку \( M \), пересекает сторону \( AC \) угла \( A \).

а) Точка \( N \) лежит на отрезке \( AB \), что означает, что \( N \) находится между точками \( A \) и \( B \) и принадлежит прямой, соединяющей эти две точки. Отрезок \( AB \) — это часть прямой, ограниченная точками \( A \) и \( B \), поэтому если \( N \) лежит на отрезке, то координаты \( N \) удовлетворяют условию, что она находится между \( A \) и \( B \). В отличие от точки \( N \), точка \( M \) не лежит на отрезке \( AB \), то есть она не принадлежит этому отрезку и расположена вне прямой, проходящей через \( A \) и \( B \).

Это видно на рисунке, где \( N \) находится на линии между \( A \) и \( B \), а \( M \) расположена выше этой линии. Таким образом, \( N \in AB \), а \( M \notin AB \). Такое расположение важно для понимания, к какой части геометрической фигуры принадлежит каждая точка.

Если рассматривать свойства отрезка, то все точки, лежащие на нем, находятся строго между его концами, а точки вне отрезка либо лежат на продолжениях прямой, либо вообще вне этой прямой, как в случае с \( M \).

б) Точка \( M \) делит прямую \( AN \) на два луча: \( MA \) и \( MN \). Прямая \( AN \) — бесконечная линия, проходящая через точки \( A \) и \( N \). Если взять точку \( M \), лежащую на этой прямой, она разбивает её на две части, каждая из которых является лучом. Луч \( MA \) начинается в точке \( M \) и идет через \( A \) бесконечно в ту сторону, а луч \( MN \) начинается в \( M \) и идет через \( N \) в противоположную сторону.

Такое разбиение прямой на два луча происходит всегда, когда точка лежит на самой прямой, но не совпадает с концами отрезка. Это позволяет рассматривать части прямой как отдельные лучи, что удобно для анализа пересечений и взаимного расположения фигур.

На рисунке видно, что \( M \) находится между \( A \) и \( N \), поэтому лучи \( MA \) и \( MN \) исходят из \( M \) в разные стороны, покрывая всю прямую \( AN \).

в) Рассмотрим три случая взаимного расположения отрезка и луча. В первом случае отрезок и луч не пересекаются, то есть у них нет общих точек. На рисунке точка \( M \) расположена ниже отрезка \( AB \), и луч, исходящий из \( N \), направлен так, что не пересекается с отрезком. Это означает, что множество общих точек пусто: \( AB \cap луч = \emptyset \).

Во втором случае отрезок лежит на луче. Это происходит, когда все точки отрезка принадлежат лучу. Например, если луч начинается в точке \( M \) и проходит через \( A \), \( N \) и \( B \), то отрезок \( ANB \) полностью содержится в луче \( MN \). В этом случае отрезок и луч совпадают по части, и у них бесконечно много общих точек.

В третьем случае отрезок и луч имеют одну общую точку. Это происходит, когда луч и отрезок пересекаются только в одной точке, например, в точке \( B \). Тогда пересечение множеств равно этой точке: \( AB \cap луч = \{B\} \).

г) Прямая пересекает одну сторону угла, если она проходит через одну из его лучевых сторон и не касается другой. На рисунке угол образован лучами \( AN \) и \( AC \), исходящими из точки \( A \). Прямая, проходящая через точку \( M \), пересекает сторону \( AC \), но не пересекает сторону \( AN \).

Это означает, что прямая касается только одной стороны угла, что важно для определения взаимного расположения прямых и углов в геометрии. Такое расположение позволяет анализировать углы и их свойства, например, при построении перпендикуляров или биссектрис.