ГДЗ по Математике 5 Класс Часть 2 Номер 987 Мнемозина Виленкин, Жохов — Подробные Ответы

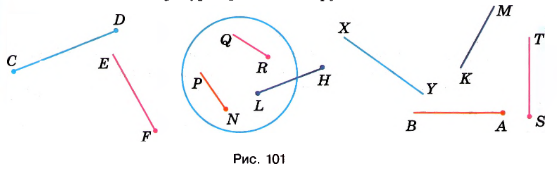
Какие отрезки, лучи и прямые на рисунке 101 пересекаются? Какие из этих фигур пересекают окружность?

Луч \(FE\) пересекает отрезок \(CD\).

Луч \(FE\) пересекает прямую \(XY\).

Лучи \(FE\) и \(AB\) пересекаются.

Луч \(NP\) пересекается с прямой \(XY\).

Лучи \(NP\) и \(RQ\) пересекаются.

Лучи \(FE\) и \(RQ\) пересекаются.

Прямая \(XY\) пересекает луч \(AB\).

Прямая \(MK\) пересекает отрезок \(AB\).

Прямые \(XY\) и \(MK\) пересекаются.

Луч \(ST\) пересекает прямую \(MK\).

Лучи \(RQ\), \(NP\), \(AB\) и отрезок \(LH\) пересекают окружность.

Луч \(FE\) пересекает отрезок \(CD\). Это означает, что луч, исходящий из точки \(F\) и проходящий через точку \(E\), пересекает отрезок, ограниченный точками \(C\) и \(D\). Пересечение луча и отрезка возможно, если существует точка, принадлежащая одновременно лучу и отрезку. Поскольку луч бесконечен в одном направлении, а отрезок ограничен двумя точками, их пересечение — это конкретная точка на отрезке \(CD\), которая лежит на линии, задаваемой лучом \(FE\).

Луч \(FE\) пересекает прямую \(XY\). Прямая \(XY\) бесконечна в обе стороны, поэтому луч \(FE\), направленный из точки \(F\) через точку \(E\), обязательно пересечет прямую \(XY\), если они не параллельны. Пересечение происходит в точке, которая принадлежит обеим фигурам — лучу и прямой. Важно, что здесь речь идет о прямой, а не об отрезке, поэтому точка пересечения может находиться в любом месте на линии \(XY\).

Лучи \(FE\) и \(AB\) пересекаются. Лучи — это полу-бесконечные линии, начинающиеся в одной точке и идущие в одном направлении. Для того чтобы лучи \(FE\) и \(AB\) пересеклись, должна существовать общая точка, принадлежащая обоим лучам. Это возможно, если направления лучей пересекаются, а не параллельны или совпадают. Пересечение лучей означает, что они имеют хотя бы одну общую точку, которая лежит на обоих лучах.

Луч \(NP\) пересекается с прямой \(XY\). Луч \(NP\), исходящий из точки \(N\) через точку \(P\), пересекает прямую \(XY\), если они не параллельны. Поскольку прямая бесконечна в обе стороны, и луч бесконечен в одном направлении, пересечение происходит в точке, которая принадлежит обеим фигурам. Если же луч и прямая параллельны, пересечения не будет.

Лучи \(NP\) и \(RQ\) пересекаются. Для того чтобы два луча пересеклись, необходимо, чтобы они имели общую точку, которая лежит в направлении обоих лучей. Если лучи исходят из разных точек и направлены так, что их линии пересекаются, то существует точка пересечения. Если направления лучей параллельны или расходятся, то пересечения не будет.

Лучи \(FE\) и \(RQ\) пересекаются. Аналогично предыдущему пункту, пересечение двух лучей возможно при наличии общей точки на обоих лучах. Это значит, что линии, вдоль которых направлены лучи, пересекаются, и точка пересечения лежит в направлении обоих лучей.

Прямая \(XY\) пересекает луч \(AB\). Прямая \(XY\) бесконечна в обе стороны, луч \(AB\) — полу-бесконечен. Для пересечения необходимо, чтобы линии, на которых лежат прямая и луч, имели общую точку, принадлежащую лучу \(AB\). Если они параллельны и не совпадают, пересечения нет. Если же они пересекаются, точка пересечения принадлежит обеим фигурам.

Прямая \(MK\) пересекает отрезок \(AB\). Отрезок \(AB\) ограничен точками \(A\) и \(B\), прямая \(MK\) бесконечна. Пересечение происходит, если линия \(MK\) проходит через область, ограниченную отрезком \(AB\), то есть существует точка, принадлежащая и отрезку, и прямой. Если прямая параллельна отрезку и не совпадает, пересечения нет.

Прямые \(XY\) и \(MK\) пересекаются. Две прямые в пространстве либо параллельны, либо пересекаются в одной точке, либо совпадают. Здесь утверждается, что они пересекаются, значит, существует единственная точка, принадлежащая обеим прямым. Эта точка является их точкой пересечения.

Луч \(ST\) пересекает прямую \(MK\). Луч \(ST\), исходящий из точки \(S\) через точку \(T\), пересекает прямую \(MK\), если линии, на которых они лежат, пересекаются, и точка пересечения принадлежит направлению луча \(ST\). Если луч направлен в сторону от точки пересечения, пересечение существует, иначе нет.

Лучи \(RQ\), \(NP\), \(AB\) и отрезок \(LH\) пересекают окружность. Пересечение лучей и отрезков с окружностью означает, что существует хотя бы одна точка, принадлежащая одновременно окружности и каждому из этих геометрических объектов. Окружность — множество точек, равноудаленных от центра. Если луч или отрезок проходят через область окружности, они пересекаются в одной или двух точках, в зависимости от положения и направления.