ГДЗ по Математике 5 Класс Часть 2 Номер 965 Мнемозина Виленкин, Жохов — Подробные Ответы

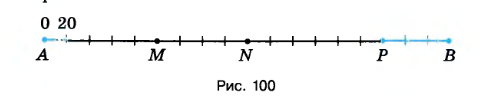
На рисунке 100 изображена шкала расстояний от города А до города В. Каждое деление шкалы соответствует расстоянию 20 км. Точками \(M, N, P\) отмечены расстояния, которые прошла автомашина через каждый час, двигаясь из города \(A\) в город \(B\). Определите:
а) чему равно расстояние от города \(A\) до города \(B\);
б) какое расстояние прошла автомашина за первые 2 ч; за вторые 2 ч;
в) на каком расстоянии от города \(B\) была автомашина через 2 ч после выхода из города \(A\);
г) какое расстояние прошла автомашина за 3 ч;
д) с какой средней скоростью шла автомашина в первые 2 ч; во вторые 2 ч.

а) Расстояние от города \( A \) до города \( B \) равно \( 20 \cdot 18 = 360 \) км, так как от \( A \) до \( B \) 18 делений по 20 км.

б) За первые два часа автомашина прошла \( 20 \cdot 9 = 180 \) км; за вторые два часа автомашина прошла \( 20 \cdot 9 = 180 \) км.

в) Через 2 ч после выхода из города \( A \) автомашина была в 180 км от города \( B \).

г) За 3 ч автомашина прошла \( 20 \cdot 15 = 300 \) км.

д) В первые 2 ч автомашина шла со средней скоростью: \( \frac{180}{2} = 90 \) км/ч.
Во вторые 2 ч автомашина шла со средней скоростью: \( \frac{180}{2} = 90 \) км/ч.

а) Расстояние между городами \( A \) и \( B \) определяется по количеству делений на шкале и длине каждого деления. В условии указано, что от \( A \) до \( B \) расположено 18 делений, каждое из которых соответствует 20 км. Чтобы найти полное расстояние, нужно умножить количество делений на длину одного деления. Таким образом, вычисляем: \( 20 \cdot 18 = 360 \) км. Это означает, что город \( B \) находится на расстоянии 360 км от города \( A \).

Такой способ вычисления основан на прямом пропорциональном отношении между количеством делений и общим расстоянием. Если бы количество делений или длина одного деления изменились, то и расстояние между городами также изменилось бы. В данном случае, зная точные параметры шкалы, можно легко получить искомое расстояние.

б) Для определения пройденного пути за первые два часа нужно умножить скорость движения на время. Из условия видно, что за каждый час автомашина проходит 9 делений, а каждое деление равно 20 км. Следовательно, за два часа машина проезжает \( 9 \cdot 2 = 18 \) делений. Теперь вычислим расстояние: \( 20 \cdot 9 = 180 \) км за два часа. Аналогично, за вторые два часа машина прошла такое же расстояние, поскольку скорость и время те же, то есть также \( 180 \) км.

Этот расчет показывает, что скорость машины постоянна и равна \( \frac{180}{2} = 90 \) км/ч. Таким образом, за каждые два часа машина проезжает одинаковое расстояние, что подтверждается равенством \( 20 \cdot 9 = 180 \) км.

в) Через 2 часа после выезда из города \( A \) машина находится на расстоянии 180 км от города \( B \). Это можно понять, если учесть, что общее расстояние между городами равно 360 км, а за первые два часа машина проехала 180 км. Значит, расстояние от машины до города \( B \) равно \( 360 — 180 = 180 \) км.

Это показывает, что машина движется равномерно, и через 2 часа после начала пути она находится ровно посередине между городами \( A \) и \( B \). Такой вывод подтверждается расчетами пройденного пути и оставшегося расстояния.

г) За 3 часа машина проехала расстояние, которое можно найти, умножив количество делений, пройденных за это время, на длину одного деления. Из условия видно, что за 3 часа пройдено 15 делений. Тогда расстояние равно \( 20 \cdot 15 = 300 \) км.

Этот расчет основан на постоянной скорости машины, которая позволяет определить путь за любое время, умножая количество делений на длину одного деления. Таким образом, за 3 часа машина преодолела 300 км.

д) Для нахождения средней скорости за первые 2 часа нужно разделить пройденное расстояние на время движения. Из предыдущих пунктов известно, что за 2 часа машина проехала 180 км. Следовательно, средняя скорость равна \( \frac{180}{2} = 90 \) км/ч.

Аналогично, за вторые 2 часа машина также прошла 180 км, значит средняя скорость за этот промежуток времени такая же и равна \( \frac{180}{2} = 90 \) км/ч. Это подтверждает, что скорость автомобиля была постоянной на протяжении всего времени движения.