ГДЗ по Математике 5 Класс Часть 2 Номер 958 Мнемозина Виленкин, Жохов — Подробные Ответы

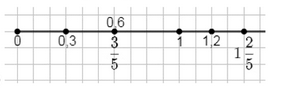
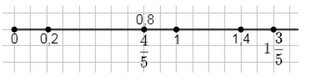
Приняв за единичный отрезок длину 10 клеток тетради, отметьте на луче точки, координаты которых равны:

а) 0; 1; 0,3; \(\frac{3}{5}\); 0,6; \(1\frac{2}{5}\); 1,2;

б) 0; 1; 0,2; \(\frac{4}{5}\); 0,8; \(1\frac{3}{5}\); 1,4.

а) Длина отрезка \(0,6 = 0,6 \times 10 = 6\) клеток.

Длина отрезка \(1 \frac{1}{5} = \frac{6}{5} = 1,2\), значит \(1,2 \times 10 = 12\) клеток.

б) Длина отрезка \(0,8 = 0,8 \times 10 = 8\) клеток.

Длина отрезка \(1 \frac{3}{5} = \frac{8}{5} = 1,6\), значит \(1,6 \times 10 = 16\) клеток.

а) В условии сказано, что единичный отрезок равен 10 клеткам. Это значит, что длина отрезка, равная 1, соответствует 10 клеткам на изображении. Для вычисления длины любого дробного или смешанного числа в клетках нужно умножить это число на 10.

Для первого отрезка дано значение 0,6. Чтобы найти длину в клетках, умножаем \(0,6 \times 10\), что равно 6 клеткам. Это значит, что отрезок длиной 0,6 занимает 6 клеток на сетке. Аналогично, для второго отрезка дано смешанное число \(1 \frac{1}{5}\). Преобразуем его в неправильную дробь: \(1 \frac{1}{5} = \frac{6}{5}\). Теперь умножаем на 10: \(\frac{6}{5} \times 10 = \frac{6 \times 10}{5} = 12\) клеток. Таким образом, отрезок длиной \(1 \frac{1}{5}\) занимает 12 клеток на сетке.

Таким образом, чтобы найти длину отрезка в клетках, сначала нужно перевести смешанное число в неправильную дробь или оставить десятичное, а затем умножить на 10, так как 1 единичный отрезок равен 10 клеткам. Это универсальный способ для любых данных чисел на данной сетке.

б) Аналогично первому пункту, единичный отрезок равен 10 клеткам. Для вычисления длины отрезка нужно умножить его числовое значение на 10, чтобы получить длину в клетках.

Для первого отрезка задано число 0,8. Умножаем \(0,8 \times 10 = 8\) клеток. Значит, отрезок длиной 0,8 занимает 8 клеток на сетке. Для второго отрезка дано смешанное число \(1 \frac{3}{5}\). Переведём его в неправильную дробь: \(1 \frac{3}{5} = \frac{8}{5}\). Теперь умножаем на 10: \(\frac{8}{5} \times 10 = \frac{8 \times 10}{5} = 16\) клеток. Значит, отрезок длиной \(1 \frac{3}{5}\) занимает 16 клеток.

Таким образом, для любого числа, заданного на сетке, длину в клетках можно найти, умножив это число на 10. Это связано с тем, что единичный отрезок равен 10 клеткам, и поэтому длина любого отрезка пропорциональна этому значению.