ГДЗ по Математике 5 Класс Часть 2 Номер 94 Мнемозина Виленкин, Жохов — Подробные Ответы

Отметьте на координатном луче точки, координаты которых равны:

а) \(\frac{1}{5}; \frac{2}{5}; \frac{3}{5}; \frac{4}{5}\);

б) \(\frac{1}{8}; \frac{3}{8}; \frac{5}{8}; \frac{7}{8}\).

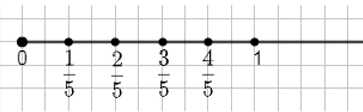
а) Единичный отрезок равен 10 клеткам, тогда дроби на отрезке будут с знаменателем 5, так как \( \frac{10}{2} = 5 \). Отметки:
0, \( \frac{1}{5} \), \( \frac{2}{5} \), \( \frac{3}{5} \), \( \frac{4}{5} \), 1.

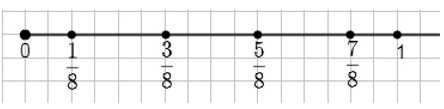
б) Единичный отрезок равен 16 клеткам, тогда дроби на отрезке будут с знаменателем 8, так как \( \frac{16}{2} = 8 \). Отметки:
0, \( \frac{1}{8} \), \( \frac{3}{8} \), \( \frac{5}{8} \), \( \frac{7}{8} \), 1.

а) Единичный отрезок на рисунке разбит на 10 клеток, что означает, что длина всего отрезка равна 10 условным единицам, каждая из которых соответствует одной клетке. Чтобы представить дроби с одинаковым знаменателем, нужно определить, на сколько частей делится единичный отрезок. В данном случае дроби представлены с знаменателем 5, так как каждые 2 клетки соответствуют одной пятой части отрезка. Это объясняется тем, что \( \frac{10}{2} = 5 \), то есть 10 клеток делятся на 5 равных частей по 2 клетки каждая.

Далее на отрезке отмечены точки, соответствующие дробям \( \frac{1}{5} \), \( \frac{2}{5} \), \( \frac{3}{5} \), \( \frac{4}{5} \), и конечная точка 1, которая соответствует целому отрезку. Это значит, что каждая дробь указывает на положение точки, находящейся на расстоянии, кратном \( \frac{1}{5} \) длины отрезка от начала. Таким образом, дроби равномерно распределены по отрезку, и можно точно определить их значения, исходя из количества клеток.

В итоге, единичный отрезок, равный 10 клеткам, разбит на 5 равных частей, и дроби с знаменателем 5 отображают доли от этого отрезка. Отметки на отрезке записываются как 0, \( \frac{1}{5} \), \( \frac{2}{5} \), \( \frac{3}{5} \), \( \frac{4}{5} \), 1, что соответствует равномерному делению отрезка на части по 2 клетки каждая.

б) Во втором случае единичный отрезок равен 16 клеткам, что означает, что длина отрезка составляет 16 условных единиц. Для удобства и точности дробей на отрезке выбраны дроби с знаменателем 8, так как 16 клеток можно разбить на 8 равных частей по 2 клетки каждая. Это следует из вычисления \( \frac{16}{2} = 8 \), то есть отрезок делится на 8 равных частей.

На рисунке отмечены дроби с нечетными числителями: \( \frac{1}{8} \), \( \frac{3}{8} \), \( \frac{5}{8} \), \( \frac{7}{8} \), а также точки 0 и 1, которые обозначают начало и конец отрезка соответственно. Эти дроби показывают промежуточные точки, расположенные на расстояниях, кратных \( \frac{1}{8} \) длины отрезка. Таким образом, каждая дробь указывает на положение точки, находящейся на определённом числе клеток от начала отрезка.

В результате, единичный отрезок, равный 16 клеткам, разбит на 8 равных частей, и дроби с знаменателем 8 представляют доли от этого отрезка. Отметки на отрезке выглядят следующим образом: 0, \( \frac{1}{8} \), \( \frac{3}{8} \), \( \frac{5}{8} \), \( \frac{7}{8} \), 1, что отражает равномерное деление отрезка на части по 2 клетки каждая.