ГДЗ по Математике 5 Класс Часть 2 Номер 93 Мнемозина Виленкин, Жохов — Подробные Ответы

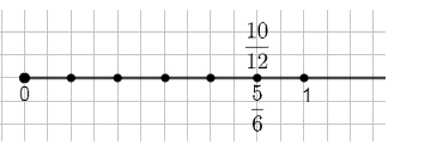
Единичный отрезок равен 12 клеткам. Отметьте на координатном луче точки \(A\left(\frac{5}{6}\right)\) и \(B\left(\frac{10}{12}\right)\). Объясните результат.

Разделим единичный отрезок на 6 равных частей и 5 из них закрасим. Закрашенная часть составляет \( \frac{5}{6} \) отрезка.

Потом каждую шестую часть отрезка разделим еще на 2 равные части. Тогда весь отрезок будет разделен на \(6 \cdot 2 = 12\) частей, а в пяти закрашенных частях отрезка будет \(5 \cdot 2 = 10\) частей. Значит, закрашено \( \frac{10}{12} \) отрезка.

Следовательно, \( \frac{5}{6} = \frac{10}{12} \).

Разделим единичный отрезок на 6 равных частей. Это значит, что каждый маленький отрезок будет равен \( \frac{1}{6} \) длины всего отрезка. Если мы закрасим 5 из этих 6 частей, то закрашенная длина будет равна сумме 5 таких частей, то есть \( 5 \cdot \frac{1}{6} = \frac{5}{6} \). Таким образом, закрашенная часть составляет именно \( \frac{5}{6} \) всего отрезка. Это простой способ выразить часть целого через дробь, где числитель — количество выделенных частей, а знаменатель — общее количество равных частей.

После этого каждую из шести частей мы делим ещё на 2 равные части. Это значит, что каждая шестая часть теперь состоит из двух двенадцатых части от всего отрезка, поскольку \( 6 \cdot 2 = 12 \). Таким образом, весь отрезок теперь разделён на 12 равных частей, каждая из которых равна \( \frac{1}{12} \) длины отрезка. При этом количество закрашенных частей тоже увеличивается: если изначально было закрашено 5 частей, а каждая из них теперь разделена на 2, то общее количество закрашенных частей станет \( 5 \cdot 2 = 10 \).

Теперь мы можем сказать, что закрашено 10 частей из 12, то есть закрашенная часть равна \( \frac{10}{12} \) всего отрезка. Это дробь, эквивалентная \( \frac{5}{6} \), но с другим знаменателем. Таким образом, дробь \( \frac{5}{6} \) можно представить как \( \frac{10}{12} \), что подтверждает равенство дробей. Это показывает, что при умножении числителя и знаменателя дроби на одно и то же число, значение дроби не меняется, а дробь становится с другим знаменателем, но равна исходной.