ГДЗ по Математике 5 Класс Часть 2 Номер 928 Мнемозина Виленкин, Жохов — Подробные Ответы

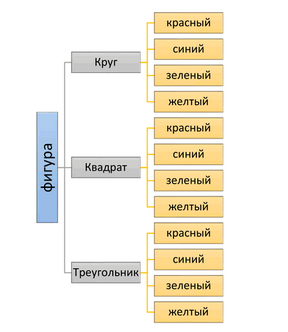
У ученика на парте три геометрические фигуры: круг, квадрат и треугольник. Ему надо выбрать одну из этих фигур и раскрасить её в один из цветов: красный, синий, зелёный или жёлтый. Сколькими способами он может это сделать?

Ученик может выбрать одну фигуру из трёх: круг, квадрат или треугольник.

Каждую фигуру можно раскрасить в один из четырёх цветов: красный, синий, зелёный или жёлтый.

Всего способов раскрасить одну фигуру: \(3 \times 4 = 12\).

Ответ: 12 способов.

Ученик выбирает одну из трёх фигур: круг, квадрат или треугольник. Это означает, что всего вариантов выбора фигуры ровно 3, так как каждая фигура уникальна и выбор только один. Этот этап важен, так как определяет, сколько различных объектов можно раскрасить. Выбор фигуры — это первый шаг в вычислении общего количества способов раскраски.

После выбора фигуры ученик должен выбрать цвет для раскраски. Цветов всего четыре: красный, синий, зелёный и жёлтый. Для каждой фигуры можно применить любой из этих цветов, то есть для каждого варианта фигуры существует 4 варианта цвета. Это значит, что количество способов раскраски одной фигуры равно количеству цветов, доступных для выбора.

Общее число способов выбрать фигуру и раскрасить её равно произведению количества фигур на количество цветов. Это происходит потому, что выбор фигуры и выбор цвета — независимые действия, и для каждого выбора фигуры можно применить любой из цветов. Таким образом, общее количество вариантов равно \(3 \times 4\). В итоге получаем, что всего существует \(12\) способов раскрасить одну фигуру в один из четырёх цветов. Ответ: 12 способов.