ГДЗ по Математике 5 Класс Часть 2 Номер 92 Мнемозина Виленкин, Жохов — Подробные Ответы

Начертите в тетради отрезок длиной в 18 клеток. С помощью этого отрезка объясните, почему:
а) \(\frac{2}{9} = \frac{4}{18}\);
б) \(\frac{5}{6} = \frac{15}{18}\).

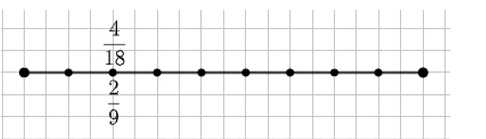
а) Разделим отрезок на 9 равных частей и закрасим 2 из них. Закрашенная часть составляет \( \frac{2}{9} \) отрезка.
Потом каждую девятую часть разделим ещё на 2 равные части. Тогда весь отрезок будет разделён на \( 9 \cdot 2 = 18 \) частей, а в двух закрашенных частях будет \( 2 \cdot 2 = 4 \) части. Значит, закрашено \( \frac{4}{18} \) отрезка.
Следовательно, \( \frac{2}{9} = \frac{4}{18} \).

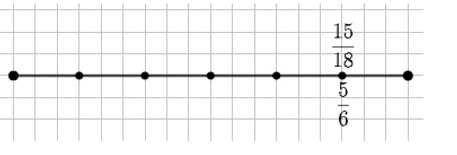
б) Разделим отрезок на 6 равных частей и закрасим 5 из них. Закрашенная часть составляет \( \frac{5}{6} \) отрезка.
Потом каждую шестую часть разделим ещё на 3 равные части. Тогда весь отрезок будет разделён на \( 6 \cdot 3 = 18 \) частей, а в пяти закрашенных частях будет \( 5 \cdot 3 = 15 \) частей. Значит, закрашено \( \frac{15}{18} \) отрезка.
Следовательно, \( \frac{5}{6} = \frac{15}{18} \).

а) Для начала рассмотрим дробь \( \frac{2}{9} \). Это означает, что отрезок разделён на 9 равных частей, и нам нужно взять 2 из них. Чтобы наглядно показать равенство дробей \( \frac{2}{9} \) и \( \frac{4}{18} \), мы сначала делим отрезок на 9 равных частей и выделяем 2 части. Это визуально показывает, что закрашенная часть составляет именно \( \frac{2}{9} \) всего отрезка.

Далее, чтобы получить дробь с знаменателем 18, каждую из девяти частей отрезка делим ещё на 2 равные части. Таким образом, весь отрезок теперь разбит на \( 9 \cdot 2 = 18 \) частей. Поскольку изначально были выделены 2 части, а каждая теперь разделена на 2, количество выделенных маленьких частей становится \( 2 \cdot 2 = 4 \). Значит, закрашено 4 части из 18, то есть \( \frac{4}{18} \). Это означает, что дроби \( \frac{2}{9} \) и \( \frac{4}{18} \) действительно равны, так как они показывают одну и ту же часть отрезка, но обозначенную разными способами.

Таким образом, мы видим, что умножение числителя и знаменателя дроби \( \frac{2}{9} \) на одно и то же число 2 даёт дробь \( \frac{4}{18} \), которая эквивалентна исходной. Это важное свойство дробей, которое позволяет сравнивать и приводить их к общему знаменателю для дальнейших вычислений.

б) Рассмотрим дробь \( \frac{5}{6} \). Она означает, что отрезок разделён на 6 равных частей, из которых 5 закрашены. Чтобы показать, что эта дробь равна \( \frac{15}{18} \), сначала делим отрезок на 6 частей и выделяем 5 из них. Это наглядно иллюстрирует, что закрашенная часть составляет \( \frac{5}{6} \) от всего отрезка.

Затем каждую из шести частей делим ещё на 3 равные части. Теперь весь отрезок состоит из \( 6 \cdot 3 = 18 \) частей. Поскольку мы выделили 5 частей, а каждая из них разбита на 3, количество выделенных маленьких частей становится \( 5 \cdot 3 = 15 \). Получается, что закрашено 15 частей из 18, то есть \( \frac{15}{18} \). Это показывает, что дроби \( \frac{5}{6} \) и \( \frac{15}{18} \) равны, так как они представляют одну и ту же часть отрезка.

Таким образом, умножение числителя и знаменателя дроби \( \frac{5}{6} \) на 3 даёт дробь \( \frac{15}{18} \), которая эквивалентна исходной. Это демонстрирует, как дроби с разными знаменателями могут быть приведены к общему знаменателю для удобства сравнения и вычислений.