ГДЗ по Математике 5 Класс Часть 2 Номер 902 Мнемозина Виленкин, Жохов — Подробные Ответы

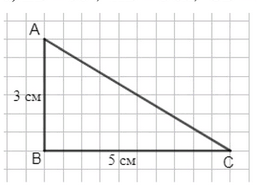
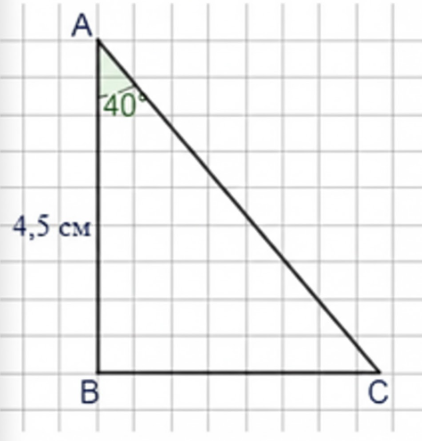
Постройте треугольник \( ABC \) с прямым углом \( B \) по следующим данным:

а) \( AB = 3 \text{ см}, CB = 5 \text{ см} \);

б) \( AB = 4,5 \text{ см}, \angle BAC = 40^\circ \).

а) По теореме Пифагора: \( AC = \sqrt{AB^2 + BC^2} = \sqrt{3^2 + 5^2} = \sqrt{9 + 25} = \sqrt{34} \approx 5{,}83 \text{ см} \).

б) В прямоугольном треугольнике \( \triangle ABC \) с прямым углом при \( B \), известен катет \( AB = 4{,}5 \text{ см} \) и угол \( \angle BAC = 40^\circ \).

Найдем гипотенузу \( AC \) через катет и угол: \( AC = \frac{AB}{\sin 40^\circ} = \frac{4{,}5}{\sin 40^\circ} \approx \frac{4{,}5}{0{,}6428} \approx 7{,}0 \text{ см} \).

Найдем второй катет \( BC = AC \cdot \cos 40^\circ = 7{,}0 \cdot 0{,}7660 \approx 5{,}36 \text{ см} \).

а) В этом задании нам дан прямоугольный треугольник \( \triangle ABC \) с прямым углом при вершине \( B \). Из условия известно, что \( AB = 3 \text{ см} \) и \( CB = 5 \text{ см} \). Нам нужно найти длину гипотенузы \( AC \). Поскольку угол \( B \) прямой, применяем теорему Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов катетов. Это основное свойство прямоугольного треугольника, которое позволяет найти неизвестную сторону, если известны две другие.

Для вычисления длины гипотенузы записываем формулу: \( AC^2 = AB^2 + BC^2 \). Подставляем известные значения: \( AC^2 = 3^2 + 5^2 = 9 + 25 = 34 \). Чтобы найти \( AC \), извлекаем квадратный корень из полученного числа: \( AC = \sqrt{34} \). Приблизительно это равно \( 5{,}83 \text{ см} \). Таким образом, гипотенуза \( AC \) чуть больше 5,8 см.

б) Во втором треугольнике также угол \( B \) прямой, при этом известен катет \( AB = 4{,}5 \text{ см} \) и угол при вершине \( A \), равный \( 40^\circ \). Здесь нужно найти длины гипотенузы \( AC \) и второго катета \( BC \). Для этого используем тригонометрические функции синуса и косинуса, которые связывают стороны и углы прямоугольного треугольника.

Первым шагом находим гипотенузу \( AC \) через известный катет и угол. Так как катет \( AB \) лежит напротив угла \( 40^\circ \), то \( \sin 40^\circ = \frac{AB}{AC} \). Отсюда выражаем \( AC = \frac{AB}{\sin 40^\circ} = \frac{4{,}5}{\sin 40^\circ} \). Значение \( \sin 40^\circ \approx 0{,}6428 \), тогда \( AC \approx \frac{4{,}5}{0{,}6428} \approx 7{,}0 \text{ см} \).

Далее, чтобы найти второй катет \( BC \), используем косинус того же угла: \( \cos 40^\circ = \frac{BC}{AC} \). Значит, \( BC = AC \cdot \cos 40^\circ \). Подставляем найденное \( AC \) и значение \( \cos 40^\circ \approx 0{,}7660 \), получаем \( BC \approx 7{,}0 \cdot 0{,}7660 = 5{,}36 \text{ см} \). Таким образом, длины сторон вычислены с помощью основных тригонометрических соотношений для прямоугольного треугольника.