ГДЗ по Математике 5 Класс Часть 2 Номер 901 Мнемозина Виленкин, Жохов — Подробные Ответы

Начертите треугольник и четырёхугольник так, чтобы:

а) треугольник был частью четырёхугольника;

б) четырёхугольник был частью треугольника.

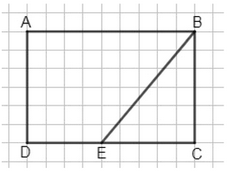
а) Треугольник \( BCE \) является частью четырехугольника \( ABCD \), так как все его вершины \( B, C, E \) лежат внутри или на границе четырехугольника \( ABCD \).

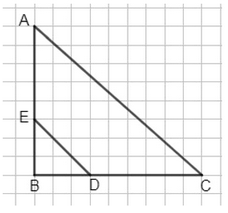
б) Четырехугольник \( ACDE \) является частью треугольника \( ABC \), поскольку все вершины \( A, C, D, E \) лежат внутри или на границе треугольника \( ABC \).

а) Треугольник \( BCE \) является частью четырехугольника \( ABCD \), поскольку все точки \( B \), \( C \) и \( E \), образующие этот треугольник, лежат внутри или на границе четырехугольника. В частности, вершины \( B \) и \( C \) — это две из вершин четырехугольника, а точка \( E \) расположена на стороне \( DC \), что гарантирует, что весь треугольник \( BCE \) находится внутри или на границе фигуры \( ABCD \). Таким образом, множество точек треугольника \( BCE \) является подмножеством множества точек четырехугольника \( ABCD \).

Для более точного понимания можно рассмотреть, что четырехугольник \( ABCD \) — это замкнутая фигура, ограниченная четырьмя сторонами \( AB \), \( BC \), \( CD \) и \( DA \). Поскольку точка \( E \) лежит на отрезке \( DC \), треугольник \( BCE \) не выходит за пределы четырехугольника. Следовательно, площадь и все внутренние точки треугольника \( BCE \) полностью содержатся в пределах \( ABCD \), что и подтверждает, что \( BCE \) является частью \( ABCD \).

б) Четырехугольник \( ACDE \) является частью треугольника \( ABC \), так как все его вершины \( A \), \( C \), \( D \) и \( E \) лежат внутри или на границах треугольника \( ABC \). В частности, вершины \( A \) и \( C \) — это вершины треугольника, а точки \( D \) и \( E \) расположены на сторонах треугольника \( ABC \) (соответственно на сторонах \( BC \) и \( AB \)). Это гарантирует, что четырехугольник \( ACDE \) полностью содержится внутри треугольника \( ABC \).

Чтобы убедиться в этом, можно проанализировать координаты точек или визуально оценить расположение. Поскольку \( D \) и \( E \) лежат на сторонах треугольника, никакая часть четырехугольника \( ACDE \) не выходит за пределы треугольника \( ABC \). Следовательно, множество точек \( ACDE \) является подмножеством множества точек \( ABC \), что и доказывает, что \( ACDE \) является частью треугольника \( ABC \).