ГДЗ по Математике 5 Класс Часть 2 Номер 89 Мнемозина Виленкин, Жохов — Подробные Ответы

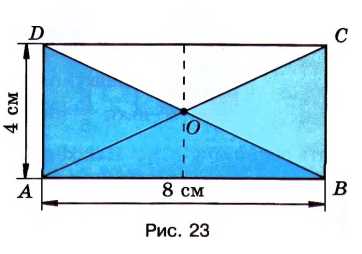
По рисунку 23 найдите площади треугольников \(ABC\), \(ACD\), \(ABO\) и \(BCO\).

\( S_{ABCD} = 4 \cdot 8 = 32 \, (\text{см}^2) \).

1) Площадь треугольника \( ABC \) равна половине площади прямоугольника \( ABCD \):
\( S_{\triangle ABC} = 32 : 2 = 16 \, (\text{см}^2) \).

2) Площадь треугольника \( ACD \) равна половине площади прямоугольника \( ABCD \):
\( S_{\triangle ACD} = 32 : 2 = 16 \, (\text{см}^2) \).

3) Площадь треугольника \( ABO \) равна четвертой части площади прямоугольника \( ABCD \):
\( S_{\triangle ABO} = 32 : 4 = 8 \, (\text{см}^2) \).

4) Площадь треугольника \( BCO \) равна четвертой части площади прямоугольника \( ABCD \):
\( S_{\triangle BCO} = 32 : 4 = 8 \, (\text{см}^2) \).

Ответ:
\( S_{\triangle ABC} = 16 \, \text{см}^2; \quad S_{\triangle ACD} = 16 \, \text{см}^2; \quad S_{\triangle ABO} = 8 \, \text{см}^2; \quad S_{\triangle BCO} = 8 \, \text{см}^2. \)

\( S_{ABCD} = 4 \cdot 8 = 32 \, (\text{см}^2) \). Это площадь прямоугольника \( ABCD \), вычисленная как произведение длины на ширину. Здесь длина равна 4 см, а ширина — 8 см. Площадь прямоугольника всегда равна произведению его соседних сторон, поэтому мы просто перемножили эти значения, получив 32 квадратных сантиметра.

1) Площадь треугольника \( ABC \) равна половине площади прямоугольника \( ABCD \), так как треугольник образован диагональю и двумя сторонами прямоугольника. Диагональ делит прямоугольник на два равных по площади треугольника. Следовательно, площадь треугольника \( ABC \) будет равна половине площади всего прямоугольника: \( S_{\triangle ABC} = \frac{32}{2} = 16 \, (\text{см}^2) \). Это объясняется тем, что диагональ делит прямоугольник на две равные части.

2) Аналогично площадь треугольника \( ACD \) равна половине площади прямоугольника \( ABCD \), поскольку он является вторым треугольником, образованным той же диагональю. Поскольку диагональ делит прямоугольник на два равных треугольника, площадь \( ACD \) также равна: \( S_{\triangle ACD} = \frac{32}{2} = 16 \, (\text{см}^2) \). Таким образом, оба треугольника, образованные диагональю, имеют одинаковую площадь.

3) Площадь треугольника \( ABO \) равна четвертой части площади прямоугольника \( ABCD \). Точка \( O \) — это точка пересечения диагоналей, которая делит прямоугольник на четыре равных треугольника. Поскольку диагонали прямоугольника пересекаются и делят его на четыре равных по площади треугольника, площадь \( ABO \) равна: \( S_{\triangle ABO} = \frac{32}{4} = 8 \, (\text{см}^2) \). Это значит, что каждый из четырёх треугольников, образованных диагоналями, занимает равную часть площади прямоугольника.

4) Аналогично площадь треугольника \( BCO \) равна четвертой части площади прямоугольника \( ABCD \), так как он также один из четырёх треугольников, образованных пересечением диагоналей. Площадь этого треугольника равна: \( S_{\triangle BCO} = \frac{32}{4} = 8 \, (\text{см}^2) \). Таким образом, все четыре треугольника, образованные диагоналями, имеют одинаковую площадь, равную одной четвертой площади прямоугольника.

Ответ:
\( S_{\triangle ABC} = 16 \, \text{см}^2; \quad S_{\triangle ACD} = 16 \, \text{см}^2; \quad S_{\triangle ABO} = 8 \, \text{см}^2; \quad S_{\triangle BCO} = 8 \, \text{см}^2. \)