ГДЗ по Математике 5 Класс Часть 2 Номер 886 Мнемозина Виленкин, Жохов — Подробные Ответы

Отметьте на луче каждый элемент множества:

а) \(\{2, 4, 9, 5, 7, 11\}\);

б) \(\{3, 8, 5, 10, 6\}\).

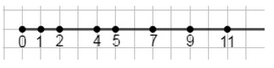
а) Множество \( \{2, 4, 9, 5, 7, 11\} \) на числовой оси: точки расположены в порядке возрастания \( 2, 4, 5, 7, 9, 11 \).

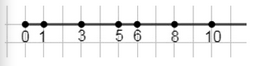
б) Множество \( \{3, 8, 5, 10, 6\} \) на числовой оси: точки расположены в порядке возрастания \( 3, 5, 6, 8, 10 \).

а) Рассмотрим множество \( \{2, 4, 9, 5, 7, 11\} \). Чтобы изобразить его на числовой оси, необходимо сначала упорядочить элементы по возрастанию. Это важно, потому что на числовой оси точки располагаются слева направо в порядке увеличения значений. Упорядоченное множество будет выглядеть так: \( 2, 4, 5, 7, 9, 11 \). Затем каждое из этих чисел отмечается точкой на соответствующем месте оси. Таким образом, на оси последовательно расположены точки, соответствующие значениям 2, 4, 5, 7, 9 и 11.

При построении множества на оси важно понимать, что порядок записи элементов в самом множестве не влияет на расположение точек. Множество — это неупорядоченный набор элементов, но для наглядного изображения на числовой оси мы всегда располагаем их в возрастающем порядке. Это позволяет ясно увидеть расстояния между числами и их относительное расположение. Например, между 2 и 4 есть промежуток, между 4 и 5 — меньший, а между 9 и 11 — больший, что видно на графике.

Таким образом, изображение множества на числовой оси — это процесс упорядочивания элементов по возрастанию и нанесения соответствующих точек. Это помогает визуально оценить распределение элементов и понять, как они соотносятся друг с другом по величине.

б) Рассмотрим множество \( \{3, 8, 5, 10, 6\} \). Аналогично первому случаю, для построения на числовой оси нужно упорядочить элементы по возрастанию. Упорядоченное множество будет: \( 3, 5, 6, 8, 10 \). После этого каждое число отмечается точкой на оси в соответствующем месте. Получается, что точки расположены слева направо в порядке увеличения значений, начиная с 3 и заканчивая 10.

Этот порядок важен для наглядности и правильного понимания расположения элементов множества. Если бы мы не упорядочили элементы, точки на оси могли бы быть разбросаны без логической последовательности, что затруднило бы восприятие. Упорядочивание позволяет увидеть, как близко или далеко друг от друга находятся элементы множества. Например, между 5 и 6 расстояние меньше, чем между 6 и 8, что отражено на оси.

Таким образом, для любого множества, чтобы изобразить его на числовой оси, нужно упорядочить элементы по возрастанию и затем нанести их как точки на ось. Это стандартный способ визуализации числовых множеств, который помогает лучше понять структуру и взаимное расположение элементов.