ГДЗ по Математике 5 Класс Часть 2 Номер 885 Мнемозина Виленкин, Жохов — Подробные Ответы

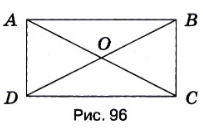
Запишите с помощью фигурных скобок множество треугольников, изображённых на рисунке 96. Сколько элементов в этом множестве?

Множество треугольников, изображенных на рисунке 96: \(\{\triangle AOB; \triangle BOC; \triangle COD; \triangle AOD; \triangle ABC; \triangle BCD; \triangle ACD; \triangle ABD\}\).

В этом множестве восемь элементов.

Множество треугольников, изображенных на рисунке 96, состоит из восьми элементов: \(\triangle AOB\), \(\triangle BOC\), \(\triangle COD\), \(\triangle AOD\), \(\triangle ABC\), \(\triangle BCD\), \(\triangle ACD\), \(\triangle ABD\). Каждое из этих треугольников образовано тремя точками, которые соединены отрезками, образующими замкнутую фигуру с тремя сторонами. Важно понять, что все эти треугольники выделяются по-разному, то есть каждая тройка точек уникальна и не повторяется в другом треугольнике.

Первый набор треугольников — это те, которые включают точку \(O\), которая, вероятно, является центром или особой точкой внутри фигуры. К ним относятся \(\triangle AOB\), \(\triangle BOC\), \(\triangle COD\), \(\triangle AOD\). Эти четыре треугольника формируются из пар соседних вершин многоугольника и точки \(O\), что позволяет разбить фигуру на части, связанные с этой центральной точкой. Такой способ разбиения часто используется для нахождения площади или анализа структуры многоугольника.

Второй набор треугольников — это те, которые образуются только вершинами многоугольника, без включения точки \(O\). Это \(\triangle ABC\), \(\triangle BCD\), \(\triangle ACD\), \(\triangle ABD\). Они представляют собой треугольники, образованные вершинами исходного многоугольника, и их выделение важно для изучения геометрических свойств самой фигуры, таких как углы, стороны и взаимное расположение точек. Таким образом, все восемь треугольников вместе дают полное представление о разбиении и структуре фигуры, изображенной на рисунке.