ГДЗ по Математике 5 Класс Часть 2 Номер 860 Мнемозина Виленкин, Жохов — Подробные Ответы

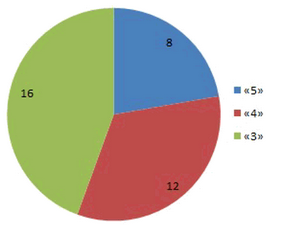
В классе 36 учеников. По математике за четверть отметку «5» имеют 8 человек, отметку «4» — 12 человек, а остальные — отметку «3». Постройте круговую диаграмму.

Так как в классе 36 учеников, то на одного ученика приходится \( \frac{360}{36} = 10^\circ \).

Значит, на отметку «5» приходится \( 8 \cdot 10 = 80^\circ \);

на отметку «4» — \( 12 \cdot 10 = 120^\circ \);

на отметку «3» — \( (36 — 8 — 12) \cdot 10 = 16 \cdot 10 = 160^\circ \).

Так как в классе всего 36 учеников, нам нужно понять, как распределяются оценки по углам круговой диаграммы. Полный круг равен 360 градусов, и каждый ученик соответствует равной части этого круга. Чтобы найти, сколько градусов приходится на одного ученика, нужно разделить весь круг на число учеников: \( \frac{360}{36} = 10^\circ \). Это значит, что каждый ученик занимает сектор в 10 градусов на круговой диаграмме.

Далее, чтобы определить угол для каждой оценки, нужно умножить количество учеников с этой оценкой на 10 градусов. Для отметки «5» таких учеников 8, значит, угол равен \( 8 \cdot 10 = 80^\circ \). Это показывает, что сектор «5» занимает 80 градусов круга, что пропорционально числу учеников с этой отметкой.

Для отметки «4» учеников 12, поэтому угол будет \( 12 \cdot 10 = 120^\circ \). Аналогично, для отметки «3» мы сначала находим количество учеников, получивших эту оценку, вычитая из общего числа учеников тех, кто получил «5» и «4»: \( 36 — 8 — 12 = 16 \). Затем умножаем на 10 градусов: \( 16 \cdot 10 = 160^\circ \). Таким образом, сектор «3» занимает 160 градусов круга, что отражает количество учеников с этой оценкой.