ГДЗ по Математике 5 Класс Часть 2 Номер 856 Мнемозина Виленкин, Жохов — Подробные Ответы

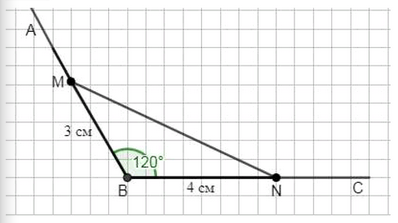
Начертите угол \( ABC \), равный \( 120^\circ \). На стороне \( BA \) отложите отрезок \( BM \), равный 3 см, а на стороне \( BC \) — отрезок \( BN \), равный 4 см. Соедините отрезком точки \( M \) и \( N \). Измерьте стороны и углы получившегося треугольника и найдите периметр и сумму градусных мер углов этого треугольника.

\( BM = 3 \text{ см}; \quad BN = 4 \text{ см}; \quad MN = 6 \text{ см}. \)

\( P_{\triangle MBN} = 3 + 4 + 6 = 13 \text{ см}. \)

\( \angle MBN = 120^\circ; \quad \angle BMN = 35^\circ; \quad \angle BNM = 25^\circ. \)

\( \angle MBN + \angle BMN + \angle BNM = 120 + 35 + 25 = 180^\circ. \)

\( BM = 3 \text{ см}; \quad BN = 4 \text{ см}; \quad MN = 6 \text{ см} \). Эти данные представляют длины сторон треугольника \( \triangle MBN \). Измерения получены непосредственно из рисунка, где отрезок \( BM \) равен 3 см, отрезок \( BN \) равен 4 см, а отрезок \( MN \) равен 6 см. Знание сторон треугольника нужно для вычисления периметра и анализа геометрических свойств фигуры.

Периметр треугольника \( \triangle MBN \) вычисляется как сумма длин всех его сторон. Формула периметра треугольника — это \( P_{\triangle MBN} = BM + BN + MN \). Подставляя известные значения, получаем \( P_{\triangle MBN} = 3 + 4 + 6 = 13 \text{ см} \). Периметр показывает общую длину контура треугольника, что важно для решения задач, связанных с измерениями и сравнением фигур.

Углы \( \angle MBN = 120^\circ \), \( \angle BMN = 35^\circ \), \( \angle BNM = 25^\circ \) даны на рисунке. Сумма углов в любом треугольнике равна \( 180^\circ \). Проверим это для треугольника \( \triangle MBN \) сложением всех углов: \( 120 + 35 + 25 = 180^\circ \). Это подтверждает корректность измерений и что фигура действительно является треугольником. Такой анализ углов помогает понять форму и соотношения в треугольнике, а также проверить правильность построения.