ГДЗ по Математике 5 Класс Часть 2 Номер 855 Мнемозина Виленкин, Жохов — Подробные Ответы

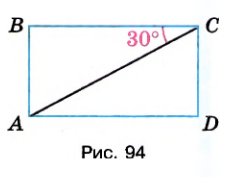
\( ABCD \) — прямоугольник, \( \angle ACB = 30^\circ \) (рис. 94). Найдите градусную меру углов: \( ACD, BAC, CAD \).

Углы в прямоугольнике по \(90^\circ\).

Сумма всех углов треугольника равна \(180^\circ\).

1) \(\angle ACD = \angle BCD — \angle ACB = 90 — 30 = 60^\circ\).

2) \(\angle CAD = 180^\circ — \angle ACD — \angle ADC = 180 — 60 — 90 = 30^\circ\).

3) \(\angle BAC = \angle BAD — \angle CAD = 90 — 30 = 60^\circ\).

Ответ: \(\angle ACD = 60^\circ\); \(\angle CAD = 30^\circ\); \(\angle BAC = 60^\circ\).

Углы в прямоугольнике равны \(90^\circ\), это базовое свойство, которое мы используем для нахождения других углов. Рассмотрим треугольник, образованный точками \(A\), \(C\), и \(D\). Известно, что сумма углов любого треугольника равна \(180^\circ\). Это фундаментальное правило геометрии, которое позволит нам вычислить неизвестные углы через известные.

1) Рассмотрим угол \(\angle ACD\). Он равен разности углов \(\angle BCD\) и \(\angle ACB\). Угол \(\angle BCD\) — это угол прямоугольника, равный \(90^\circ\), а угол \(\angle ACB\) задан как \(30^\circ\). Значит, чтобы найти \(\angle ACD\), нужно из \(90^\circ\) вычесть \(30^\circ\), то есть \(90^\circ — 30^\circ = 60^\circ\). Таким образом, \(\angle ACD = 60^\circ\). Это первый найденный угол, который мы будем использовать далее.

2) Теперь найдем угол \(\angle CAD\). Для этого используем сумму углов треугольника \(ACD\), которая равна \(180^\circ\). Из этой суммы вычитаем уже известные углы \(\angle ACD = 60^\circ\) и \(\angle ADC = 90^\circ\) (так как \(\angle ADC\) — угол прямоугольника). Получаем: \(180^\circ — 60^\circ — 90^\circ = 30^\circ\). Значит, \(\angle CAD = 30^\circ\). Это значение подтверждает, что треугольник \(ACD\) имеет углы \(30^\circ\), \(60^\circ\) и \(90^\circ\), что типично для прямоугольного треугольника с такими пропорциями.

3) Для угла \(\angle BAC\) используем разность углов \(\angle BAD\) и \(\angle CAD\). Угол \(\angle BAD\) равен \(90^\circ\), так как он принадлежит прямоугольнику. Мы уже нашли, что \(\angle CAD = 30^\circ\), поэтому \(\angle BAC = 90^\circ — 30^\circ = 60^\circ\). Таким образом, углы треугольника, сформированного точками \(A\), \(B\), и \(C\), равны \(30^\circ\), \(60^\circ\) и \(90^\circ\).

Ответ: \(\angle ACD = 60^\circ\); \(\angle CAD = 30^\circ\); \(\angle BAC = 60^\circ\).