ГДЗ по Математике 5 Класс Часть 2 Номер 850 Мнемозина Виленкин, Жохов — Подробные Ответы

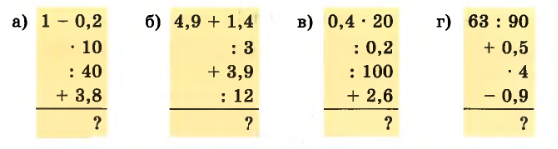
Вычислите устно:

а) \(1 — 0,2 = 0,8\);
\(0,8 \cdot 10 = 8\);
\(8 : 40 = 0,2\);
\(0,2 + 3,8 = 4\).

б) \(4,9 + 1,4 = 6,3\);
\(6,3 : 3 = 2,1\);
\(2,1 + 3,9 = 6\);
\(6 : 12 = 0,5\).

в) \(0,4 \cdot 20 = 8\);
\(8 : 0,2 = 40\);
\(40 : 100 = 0,4\);
\(0,4 + 2,6 = 3\).

г) \(63 : 90 = 0,7\);
\(0,7 + 0,5 = 1,2\);
\(1,2 \cdot 4 = 4,8\);
\(4,8 — 0,9 = 3,9\).

а) Сначала вычитаем из числа 1 число 0,2. Это простая операция вычитания десятичных дробей: \(1 — 0,2 = 0,8\). Результат показывает, сколько осталось после вычитания. Далее умножаем полученное число 0,8 на 10, что соответствует увеличению значения в 10 раз: \(0,8 \cdot 10 = 8\). Это действие часто используется для масштабирования или перевода величины в другую размерность. После этого делим 8 на 40, чтобы найти, какая часть от 40 равна 8: \(8 : 40 = 0,2\). Деление здесь показывает отношение между двумя величинами. В конце складываем результат деления с числом 3,8: \(0,2 + 3,8 = 4\). Сложение объединяет две величины, давая итоговое значение.

б) В этом пункте сначала складываем два числа: \(4,9 + 1,4 = 6,3\). Сложение десятичных дробей происходит по тому же принципу, что и с целыми числами, просто учитываем запятую. Далее делим сумму 6,3 на 3, чтобы узнать, сколько будет в одной части, если разделить поровну на три части: \(6,3 : 3 = 2,1\). Деление показывает среднее значение или долю. Потом прибавляем к результату число 3,9, чтобы получить новую сумму: \(2,1 + 3,9 = 6\). Это действие увеличивает исходное значение на заданное число. В завершение делим 6 на 12, что показывает, какую часть составляет число 6 от 12: \(6 : 12 = 0,5\).

в) Здесь сначала умножаем 0,4 на 20, что означает увеличение числа 0,4 в 20 раз: \(0,4 \cdot 20 = 8\). Это полезно для масштабирования или подсчёта общего количества при известной доле. Затем делим полученное число 8 на 0,2, чтобы выяснить, сколько раз 0,2 помещается в 8: \(8 : 0,2 = 40\). Деление на десятичную дробь увеличивает значение, так как мы делим на число меньше единицы. После этого делим 40 на 100, что уменьшает число в 100 раз: \(40 : 100 = 0,4\). Наконец, складываем 0,4 с 2,6, чтобы получить итоговое значение: \(0,4 + 2,6 = 3\).

г) В этом пункте делим 63 на 90, чтобы найти отношение этих чисел: \(63 : 90 = 0,7\). Результат показывает, какую часть от 90 составляет 63. Потом прибавляем 0,5 к полученному числу, увеличивая его: \(0,7 + 0,5 = 1,2\). Далее умножаем 1,2 на 4, что соответствует увеличению значения в 4 раза: \(1,2 \cdot 4 = 4,8\). Это может отражать масштабирование или подсчёт общей суммы. В конце вычитаем 0,9 из 4,8, уменьшая итоговое значение: \(4,8 — 0,9 = 3,9\). Вычитание показывает уменьшение величины на заданное число.