ГДЗ по Математике 5 Класс Часть 2 Номер 85 Мнемозина Виленкин, Жохов — Подробные Ответы

Найдите значение выражения:
а) \(87\,619 + 57\,994 : 271 — 15\,75 : 75\);
б) \(532 \cdot 109 — 48\,016 + 13\,631 : 43\).
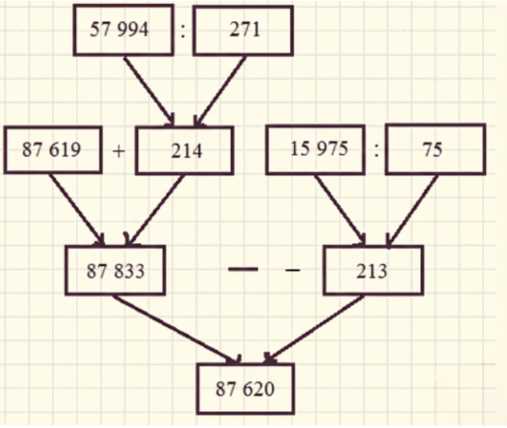
Для выражения а) составьте программу и схему вычисления.

а) \(87\,619 + \frac{57\,994}{271} — \frac{15\,975}{75} = 87\,619 + 214 — 213 = 87\,620\);

б) \(532 \cdot 109 — 48\,016 + \frac{13\,631}{43} = 57\,988 — 48\,016 + 317 = 9\,972 + 317 = 10\,289\).

Алгоритм для выражения а):
1) разделить число 57\,994 на 271;
2) разделить число 15\,975 на 75;
3) сложить 87\,619 с результатом команды 1;
4) вычесть из результата команды 3 результат команды 2.

Схема для выражения а):

а) В выражении \(87\,619 + \frac{57\,994}{271} — \frac{15\,975}{75}\) сначала необходимо выполнить деление, так как согласно порядку действий деление и умножение выполняются раньше сложения и вычитания. Делим число 57\,994 на 271. Результат деления равен 214, так как \(271 \times 214 = 57\,994\). Это позволяет заменить часть выражения \(\frac{57\,994}{271}\) на число 214.

Далее нужно разделить число 15\,975 на 75. При делении получается 213, потому что \(75 \times 213 = 15\,975\). Теперь выражение принимает вид \(87\,619 + 214 — 213\). Следующий шаг — сложение 87\,619 и 214, что дает 87\,833. После этого из полученного результата вычитаем 213, что приводит к окончательному ответу 87\,620.

Таким образом, выражение решается поэтапно, сначала выполняя деления, затем сложение и вычитание. Это соответствует правилам арифметики, где операции умножения и деления имеют приоритет над сложением и вычитанием. Такой подход помогает упростить выражение и избежать ошибок в вычислениях.

б) В выражении \(532 \cdot 109 — 48\,016 + \frac{13\,631}{43}\) первым действием будет умножение, так как оно имеет более высокий приоритет, чем сложение и вычитание. Умножаем 532 на 109, получая 57\,988, так как \(532 \times 109 = 57\,988\). Теперь выражение выглядит так: \(57\,988 — 48\,016 + \frac{13\,631}{43}\).

Следующий шаг — деление числа 13\,631 на 43. Результат равен 317, так как \(43 \times 317 = 13\,631\). Подставляем это значение в выражение: \(57\,988 — 48\,016 + 317\). Теперь выполняем вычитание: \(57\,988 — 48\,016 = 9\,972\).

Последним действием будет сложение 9\,972 и 317, которое дает итоговый результат 10\,289. Таким образом, порядок действий в выражении соблюден: сначала умножение и деление, затем сложение и вычитание. Это гарантирует правильность вычислений и упрощает процесс решения.

Алгоритм для выражения а) состоит из нескольких последовательных шагов. Сначала делим число 57\,994 на 271, получая 214. Затем делим 15\,975 на 75, получая 213. После этого складываем 87\,619 с результатом первого деления, то есть с 214, что дает 87\,833. В конце вычитаем из этого результата число, полученное во втором делении, то есть 213. Итоговое значение выражения равно 87\,620.