ГДЗ по Математике 5 Класс Часть 2 Номер 848 Мнемозина Виленкин, Жохов — Подробные Ответы

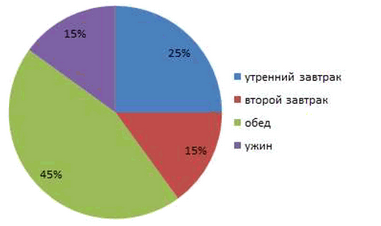
Врачи рекомендуют дневную норму питания распределить на 4 приёма: утренний завтрак — 25 %, второй завтрак — 15 %, обед — 45 % и ужин — 15 %. Постройте круговую диаграмму распределения дневной нормы питания.

1) На 1 % приходится: \(360 : 100 = 3,6^\circ\).

2) Утренний завтрак: \(3,6 \cdot 25 = 90^\circ\).

3) Второй завтрак: \(3,6 \cdot 15 = 54^\circ\).

4) Обед: \(3,6 \cdot 45 = 162^\circ\).

5) Ужин: \(3,6 \cdot 15 = 54^\circ\).

1) Для начала нужно понять, что полный круг равен \(360^\circ\), и он соответствует \(100\%\). Чтобы найти, сколько градусов соответствует одному проценту, необходимо разделить \(360^\circ\) на \(100\). Таким образом, вычисляем: \(360 : 100 = 3,6^\circ\). Это означает, что каждый процент в круговой диаграмме занимает угол в \(3,6^\circ\). Это базовый шаг, который позволяет перевести проценты в градусы для построения диаграммы.

Далее, зная, что \(1\%\) равен \(3,6^\circ\), можно вычислить углы для каждого из приёмов пищи, исходя из их процентного соотношения. Это важно для правильного отображения данных на круговой диаграмме, где каждый сектор должен соответствовать своей части общего целого.

2) Утренний завтрак занимает \(25\%\) от общего времени или количества. Чтобы узнать, сколько градусов будет занимать этот сектор на круговой диаграмме, нужно умножить значение одного процента в градусах на количество процентов, относящихся к утреннему завтраку. Получается: \(3,6 \cdot 25 = 90^\circ\). Таким образом, сектор, соответствующий утреннему завтраку, занимает угол в \(90^\circ\), что составляет четверть круга.

Этот расчет показывает, как процентное значение переводится в угол, что позволяет визуально оценить долю утреннего завтрака относительно всего времени или объема.

3) Второй завтрак занимает \(15\%\). Аналогично предыдущему шагу, умножаем \(3,6^\circ\) на \(15\), чтобы получить угол для этого сектора: \(3,6 \cdot 15 = 54^\circ\). Это значит, что второй завтрак занимает угол в \(54^\circ\) на диаграмме. Такой угол меньше, чем у утреннего завтрака, что отражает меньшую долю.

Этот способ позволяет точно показать разницу между разными категориями на диаграмме, делая визуализацию данных наглядной и понятной.

4) Обед занимает наибольшую часть — \(45\%\). Для вычисления угла умножаем \(3,6^\circ\) на \(45\): \(3,6 \cdot 45 = 162^\circ\). Это самый большой сектор на диаграмме, который занимает почти половину круга, что соответствует значительной доле обеда в общем времени или объеме.

Такой расчет позволяет выделить наиболее значимую часть данных и наглядно представить её пропорции.

5) Ужин также занимает \(15\%\), как и второй завтрак. Угол вычисляется так же: \(3,6 \cdot 15 = 54^\circ\). Это подтверждает, что ужин и второй завтрак имеют одинаковую долю на диаграмме и занимают равные сектора по \(54^\circ\) каждый.

Таким образом, все углы суммируются до \(360^\circ\), что соответствует полной круговой диаграмме и отражает правильное распределение процентов в градусах.