ГДЗ по Математике 5 Класс Часть 2 Номер 837 Мнемозина Виленкин, Жохов — Подробные Ответы

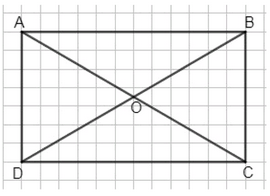
Начертите произвольный четырёхугольник \(ABCD\) и проведите прямые \(AC\) и \(BD\). Измерьте транспортиром углы \(AOB\), \(BOC\), \(COD\) и \(DOA\), где \(O\) — точка пересечения прямых \(AC\) и \(BD\). Какие из этих углов имеют одинаковую градусную меру? Сумма градусных мер каких углов равна \(180^\circ\)?

\(\angle AOB = 120^\circ; \quad \angle BOC = 60^\circ; \quad \angle COD = 120^\circ; \quad \angle DOA = 60^\circ.\)

\(\angle AOB = \angle COD; \quad \angle BOC = \angle DOA.\)

\(\angle AOB + \angle BOC = 180^\circ; \quad \angle AOB + \angle DOA = 180^\circ;\)

\(\angle BOC + \angle COD = 180^\circ; \quad \angle COD + \angle DOA = 180^\circ.\)

а) В данном задании даны углы, образованные пересечением диагоналей прямоугольника \(ABCD\) в точке \(O\). Из рисунка видно, что диагонали пересекаются, образуя четыре угла: \(\angle AOB\), \(\angle BOC\), \(\angle COD\) и \(\angle DOA\). По условию, \(\angle AOB = 120^\circ\), \(\angle BOC = 60^\circ\), \(\angle COD = 120^\circ\), \(\angle DOA = 60^\circ\). Эти углы образуют полный круг вокруг точки \(O\), поэтому сумма всех углов равна \(360^\circ\). При этом углы, расположенные напротив друг друга, равны: \(\angle AOB = \angle COD\) и \(\angle BOC = \angle DOA\). Это связано с тем, что диагонали пересекаются, образуя вертикальные углы, которые всегда равны.

б) Рассмотрим сумму углов, прилегающих друг к другу вдоль одной из диагоналей. Например, \(\angle AOB\) и \(\angle BOC\) являются смежными углами, так как они вместе образуют прямую линию \(AB\). По свойству смежных углов сумма равна \(180^\circ\), то есть \(\angle AOB + \angle BOC = 180^\circ\). Аналогично, углы \(\angle AOB\) и \(\angle DOA\) тоже лежат на одной прямой \(AD\), поэтому \(\angle AOB + \angle DOA = 180^\circ\). Это подтверждает, что диагонали пересекаются под разными углами, но углы в сумме дают прямой угол.

в) Аналогично рассмотрим углы \(\angle BOC\) и \(\angle COD\), которые лежат на прямой \(BC\). Их сумма также равна \(180^\circ\), то есть \(\angle BOC + \angle COD = 180^\circ\). Также углы \(\angle COD\) и \(\angle DOA\) лежат на прямой \(DC\), поэтому \(\angle COD + \angle DOA = 180^\circ\). Эти равенства показывают, что каждая пара углов, лежащих на одной прямой линии, образует развернутый угол, что является важным свойством пересечения диагоналей в прямоугольнике.

Таким образом, все данные углы связаны между собой через свойства вертикальных и смежных углов. Равенство противоположных углов \(\angle AOB = \angle COD\) и \(\angle BOC = \angle DOA\) объясняется тем, что они являются вертикальными углами при пересечении диагоналей. Суммы смежных углов равны \(180^\circ\), что подтверждает прямолинейность соответствующих отрезков. Эти свойства помогают понять геометрические отношения, возникающие при пересечении диагоналей в прямоугольнике.