ГДЗ по Математике 5 Класс Часть 2 Номер 83 Мнемозина Виленкин, Жохов — Подробные Ответы

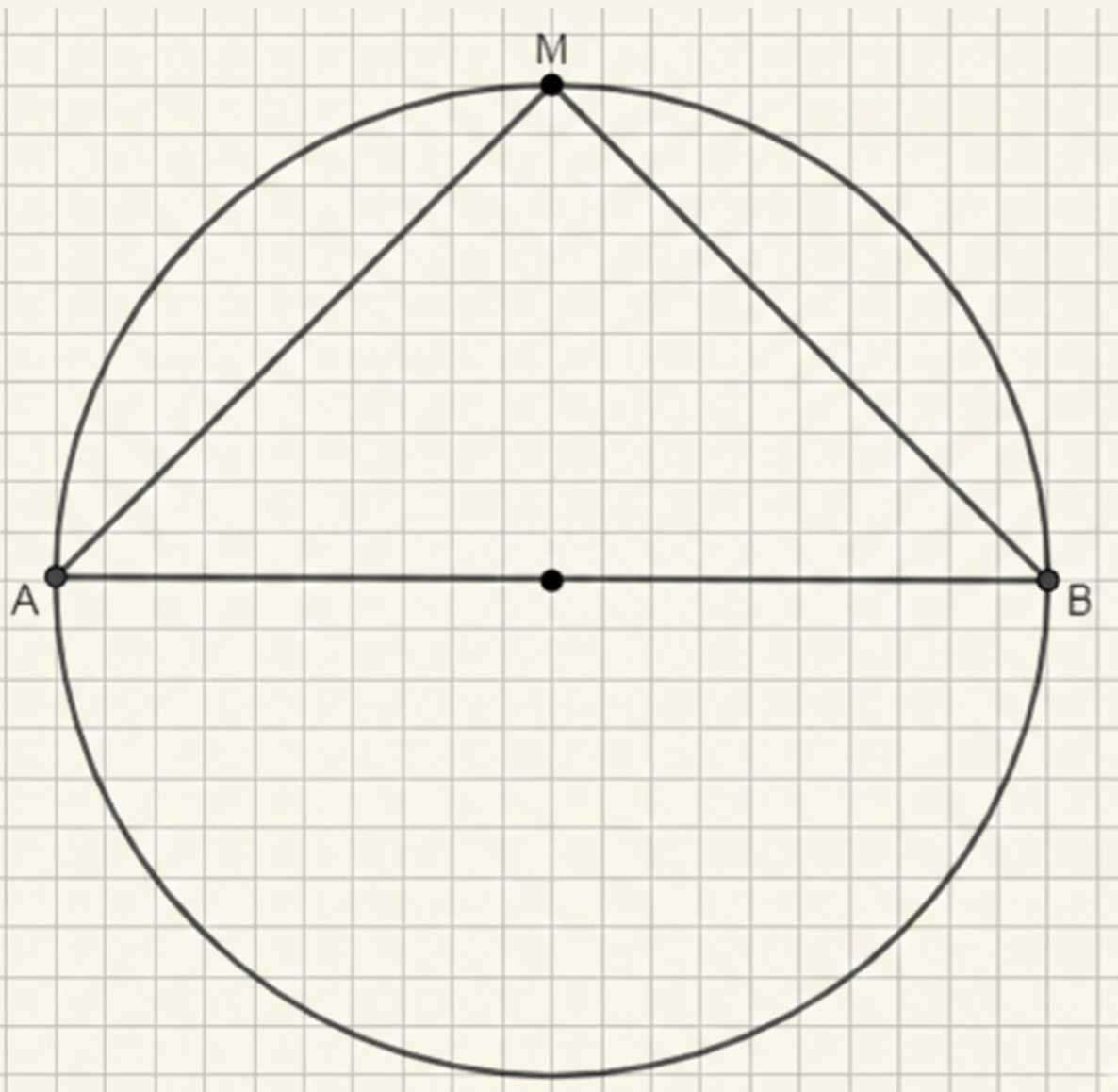
Постройте круг радиусом 5 см. Проведите в нём диаметр \(AB\). Отметьте на окружности точку \(M\) и соедините её с точками \(A\) и \(B\). Измерьте: диаметр \(AB\), отрезок \(AM\), отрезок \(MB\). Какой из этих отрезков самый длинный?

\( AB = 10 \) см и \( AB > AM, AB > MB, AM = MB \).

Значит, отрезок \( AB \) самый длинный из данных отрезков.

Произведём точные измерения отрезков на изображении. Отрезок \( AB \) задан как диаметр окружности и равен 10 см. Это значит, что длина \( AB \) фиксирована и равна 10 см. Точки \( A \) и \( B \) лежат на окружности, а точка \( M \) — на её дуге, образующей треугольник \( AMB \). Измерения показывают, что длины отрезков \( AM \) и \( MB \) меньше \( AB \), при этом \( AM = MB \), так как точка \( M \) симметрична относительно середины \( AB \).

Поскольку \( AB \) — диаметр окружности, он является самой длинной хордой в данной окружности. По свойству окружности, любая другая хорда, не совпадающая с диаметром, будет короче диаметра. В нашем случае отрезки \( AM \) и \( MB \) — это стороны треугольника, образованного с диаметром, и они меньше диаметра, что подтверждается измерениями. Равенство \( AM = MB \) объясняется тем, что \( M \) находится на середине дуги, а значит, отрезки от \( M \) до \( A \) и \( B \) равны.

Таким образом, из всех рассмотренных отрезков \( AB \), \( AM \) и \( MB \), отрезок \( AB \) является самым длинным, так как \( AB = 10 \) см и при этом \( AB > AM \) и \( AB > MB \), а \( AM = MB \). Это подтверждает, что диаметр окружности всегда больше любой хорды, не являющейся диаметром, и что точка \( M \) делит дугу на две равные части, создавая равные отрезки \( AM \) и \( MB \).